3.09.1. Паросочетания

Паросочетанием Графа G называется любое множество попарно несмежных ребер. Паросочетание графа называется Максимальным, если оно не содержится в паросочетании с большим числом ребер. Паросочетание называется Наибольшим, если оно имеет наибольшее число ребер среди всех паросочетаний данного графа. Паросочетание называется Совершенным, если оно покрывает все вершины графа, т. е. если каждая вершина графа G инцидентна некоторому ребру данного паросочетания.

Например, для графа на следующем рисунке:

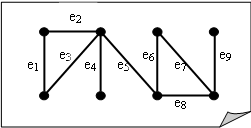· {e1, e2, e6} -- не является паросочетанием ;

· {e1, e6, e9} -- паросочетание, но не максимальное;

· {e1, e5, e7}, {e2, e6, e9} -- максимальные паросочетания, но не наибольшие;

· {e1, e4, e6, e9} -- наибольшее паросочетание. которое одновременно является совершенным.

Совершенное паросочетание существует не для всякого графа. Чаще всего паросочетания рассматриваются в двудольных графах. В двудольном графе G с долями V1 и V2 совершенным паросочетанием V1 на V2 называется паросочетание, которое покрывает все вершины доли V1.

К поиску соответствующих паросочетаний сводится решение некоторых классических задач.

Задача о свадьбах

Пусть V = {1, 2, …, N} -- множество юношей, каждый из которых знаком с некоторыми девушками из множества U = {U1, U2, …, Um}. Требуется женить наибольшее число юношей так, чтобы каждый из них женился на знакомой ему девушке.

Данная задача сводится к нахождению наибольшего паросочетания в двудольном графе G с долями V и U, в котором смежными являются вершины Vi и Uj , если соответствующие юноша и девушка знакомы, и не смежны – в противном случае. Возможность женить всех юношей означает существование в графе совершенного паросочетания V на U.

Задача о назначениях

Имеется множество исполнителей V = {1, 2, …,N}, каждый из которых может выполнить некоторые из работ множества X = {X1, X2, …, Xm}. Стоимость выполнения работы Хi исполнителем J равна Pij. Необходимо распределить исполнителей по работам так, чтобы выполнить все работы с минимальными затратами.

Ясно, что этой задаче так же отвечает соответствующий взвешенный двудольный граф. При этом возможность выполнить все работы означает существование совершенного паросочетания X на V. Для того, чтобы минимизировать затраты, необходимо искать совершенное паросочетание наименьшего веса.

< Предыдущая		Следующая >