3.06.1. Эйлеровы и гамильтоновы графы. Эйлеровы графы

Путь в графе называется Эйлеровым, если он содержит все ребра графа. Замкнутый эйлеров путь называется эйлеровым циклом. Граф, который имеет эйлеров цикл, также называется эйлеровым.

Теорема. (Эйлер). Связный граф является эйлеровым тогда и только тогда, когда степени всех его вершин четные.

Доказательство. Необходимость. Эйлеров цикл, проходя через каждую вершину, выходит из нее столько раз, сколько входит. Поэтому число ребер цикла, инцидентное каждой вершине является четным. А так как других ребер в графе, кроме принадлежащих эйлерову циклу, не существует, то степени всех вершин -- четные.

Достаточность. Пусть степени всех вершин четные. Выбрав произвольную вершину V1, начнем строить из нее цикл. Выйдем из V1 по любому ребру к следующей вершине V2. Поскольку степень V2 Четная, то существует другое (не пройденное) ребро, по которому можно перейти к следующей вершине V3. Поскольку и степень V3 четная, то из V3 Так же можно выйти по еще не пройденному ребру и т. д. Будем продолжать этот путь до тех пор, пока это возможно. Заметим, что если вычеркивать пройденные ребра, то степени проходимых вершин уменьшаются на 2 и остаются четными. Поэтому если даже в процессе построения пути мы попадем в вершину, которую уже проходили, найдется не пройденное ребро, по которому можно из этой вершины выйти. Следовательно, данный процесс может закончиться только тогда, когда мы вернемся в исходную вершину V1 И все ребра, инцидентные V1, уже будут пройдены. Таким образом, будет получен цикл.

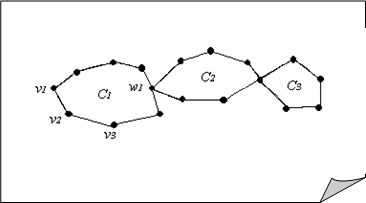Обозначим его через С1. Если цикл C1 содержит все ребра графа, то он является искомым. В противном случае, удалим из графа все ребра цикла С1. В полученном подграфе, как и в исходном, степени всех вершин останутся четными (т. к. либо не изменяется, либо уменьшается на четное число). Удалим также изолированные вершины и обозначим подграф через G1. Существуют общие вершины у G1 и построенного цикла С1 (иначе бы исходный граф не был бы связным). Пусть W1-одна из таких вершин. Начав с W1 точно также, как и раньше, построим цикл С2 в графе G1. Объединив циклы С1 и С2 получим более длинный цикл, чем С1. Если он содержит все ребра графа, то цель достигнута. В противном случае, снова удалим новый более длинный цикл из исходного графа. В оставшемся подграфеG2 построим очередной цикл С3 и т. д. Поскольку число ребер в графе конечное, рано или поздно очередной цикл СN будет содержать все ребра Gn-1. Добавляя СN к циклу, полученному на предыдущем этапе, получим эйлеров цикл.

Замечание 1. Теорема справедлива также для мульти - и псевдографов.

Замечание 2. Связный граф эйлеров тогда и только тогда, когда существует разбиение множества его ребер Е(G) на простые циклы.

Замечание 3. Если в связном графе существует ровно две вершины нечетной степени, то эйлерова цикла не существует, но существует эйлерова цепь, которая начинается в одной вершине нечетной степени, а заканчивается -- в другой (доказательство аналогично доказательству теоремы Эйлера). Если число вершин нечетной степени равно 2K, то нетрудно показать, что граф покрывается (т. е. является обьединением) K реберно-непересекающихся цепями.

Ориентированный граф называется эйлеровым, если в нем существует ориентированный эйлеров цикл, т. е. цикл, проходящий по всем дугам с соблюдением ориентации. Легко видеть, что для ориентированных графов, справедлива

Теорема. Связный ориентированный граф является эйлеровым тогда и только тогда, когда для любой его вершины V Полустепень исхода равна полстепени захода: Deg+V = deg-V.

< Предыдущая		Следующая >