3.05.6. Разрезы графа. Фундаментальная система циклов и фундаментальная система разрезов

Разделяющим множеством Графа называется такая его совокупность ребер о, удаление которых приводит к увеличению числа компонент связности графа . В частности для связного графа — это такая совокупность ребер графа , удаление которых приводит к несвязному графу. Минимальное разделяющее множество (то есть такое, что никакое его собственное подмножество разделяющим уже не является) называется Разрезом. Разрез, состоящий из одного ребра, называется Мостом.

Например, для графа на рисунке:

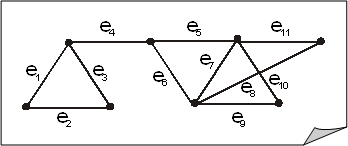
· — разделяющее множество, но не разрез;

· , , — разрезы;

· — мост;

· — не является разделяющим множеством.

Дополнением подграфа в графе будем называть граф , который имеет те же вершины, что и граф и все те ребра графа , которые не принадлежат подграфу .

Теорема. Пусть — остов графа .

1. Всякий разрез графа имеет общее ребро с .

2. Всякий цикл графа имеет общее ребро с дополнением остова в графе .

Доказательство. 1. Пусть множество ребер графа является разрезом графа . Удаление всех ребер множества разбивает некоторую компоненту связности графа на две части и . Поскольку — остов, его часть, покрывающая вершины компоненты , является деревом, в частности, связным графом и поэтому имеет ребро, соединяющее некоторую вершину с некоторой вершиной . Это ребро является общим у и .

2. Пусть теперь — некоторый цикл графа . Предположим, что он не имеет общих ребер с . Тогда целиком содержится в остове . Но это невозможно, поскольку остов есть лес, то есть граф без циклов. Теорема доказана.

Пусть дан граф . Зафиксируем некоторый его остов . Как известно (критерии дерева), если добавить к  некоторое ребро графа (удаленное при получении остова), то появится ровно один цикл. Множество циклов, полученных таким способом, называется Фундаментальной системой циклов, ассоциированной с остовом . Ясно, что все циклы, полученные таким способом, различны и их количество равно циклическому рангу .

Так, например, если — граф на предыдущем рисунке и — его остов на рисунке справа, то фундаментальная система циклов , ассоциированная с остовом , следующая:

Согласно теореме о критериях дерева (пункт d)) удаление любого ребра из остова разбивает на две компоненты связности. Пусть — вершины одной компоненты, а — другой. Если добавить к такому ребру остова другие ребра графа , соединяющие вершины с вершинами , то получим некоторый разрез графа . Множество разрезов, полученных таким способом. Называется Фундаментальной системой разрезов графа , ассоциированной с остовом . Понятно, что количество разрезов в фундаментальной системе равно числу ребер в остове, которое совпадает с рангом разрезов графа .

Для рассматриваемого графа и его остова , получаем следующую фундаментальную систему разрезов: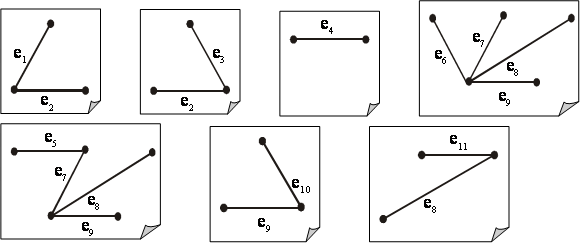

< Предыдущая		Следующая >