3.04.3. Метод поиска в ширину

Метод поиска в ширину позволяет легко найти расстояние от данной вершины до других вершин графа, и значит, определить удалённость данной вершины. Применив его для всех вершин графа, получим удалённости всех вершин, зная которые, можно найти радиус, диаметр графа, а так же центры и периферийные центры.

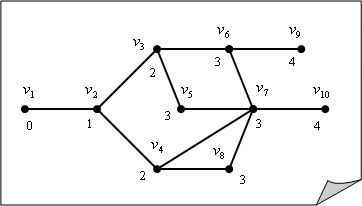
Проиллюстрируем данный метод на следующем примере (см. рис. ниже).

Суть метода заключается в расстановке меток, которая осуществляется по следующему правилу. Предположим, нужно найти расстояние от вершины V1 до других вершин. Присвоим вершине V1 метку 0. Всем вершинам, смежным с V1, присвоим метку 1. Затем всем вершинам, смежным с вершинами имеющими метку 1 (которые ещё не имеют метки), присвоим метку 2 и т. д., пока все вершины не получат метки. Легко видеть, что метка вершины будет равна расстоянию от V 1 до данной вершины, а наибольшая из меток равна удалённости вершины V 1. Так, в рассматриваемом примере e(V1) = 4. Метод позволяет так же находить кратчайшие цепи между вершинами. Если, например, нужно найти кратчайшую цепь от V1 до V10, то после расстановки меток двигаемся в обратном порядке от вершины V10, переходя каждый раз к вершине с меньшей меткой (такая обязательно найдётся; если их несколько, то выбираем любую): V10 ® V7 ® V4 ® V2 ® V1. В результате, получаем кратчайшую (V1, V10)–цепь: (V1, V2, V4, V7, V10).

Подсчёты удалённостей остальных вершин приводят к следующим результатам: e(V2)=3, e(V3)=3, e(V4)=3, e(V5)=3, e(V6)=3, e(V7)=3, e(V8)=3, e(V9)=4, e(V10)=4.

Таким образом, для данного графа G имеем: R(G)=3; D(G)=4; вершины V1, V9, V10 являются периферийными центрами, а все остальные вершины – центрами.

Выяснение вопросов связности, достижимости и расстояний на графе по матрице смежности.

Пусть G – помеченный граф, V(G) = {1, 2, … , N} и M = (Mi,J) – матрица смежности графа G. Умножим матрицу M на себя, т. е. вычислим элементы матрицы M2 и выясним их смысл. Элемент матрицы M2 в I–той строчке J–том столбце равен:

Произведения Mi,KMk,J будут равны единице только в том случае, когда вершина K является смежной с обеими вершинами I и J, т. е. если существует маршрут длины 2 соединяющий I через K с J. В остальных случаях Mi,KMk,J = 0. Поэтому есть число маршрутов длины 2, соединяющих вершину I с вершиной J. Диагональные элементы матрицы M2, в частности, совпадают со степенями соответствующих вершин. Точно так же можно показать, что элементы матрицы M3 суть количества маршрутов длины 3, соединяющие соответствующие пары вершин; элементы M4 -- количества маршрутов длины 4, и т. д.

Таким образом, расстояние между вершинами I и J равно наименьшей степени R матрицы M такой, что (I,J)–элемент матрицы Mr отличен от 0. Так как расстояния не могут быть больше N-1, где N – порядок графа, то для того, чтобы найти все расстояния и выяснить другие связанные с ними вопросы, достаточно рассмотреть степени R≤N-1. Если = 0 для всех 1 ≤ R ≤ N-1, то не существует маршрута между вершинами I и J, и значит, граф не связан.

< Предыдущая		Следующая >