3.03.2. Операции над графами
Удаление вершин (см. выше). Удаление ребра (при этом концы ребра не удаляются), а также добавление ребра. 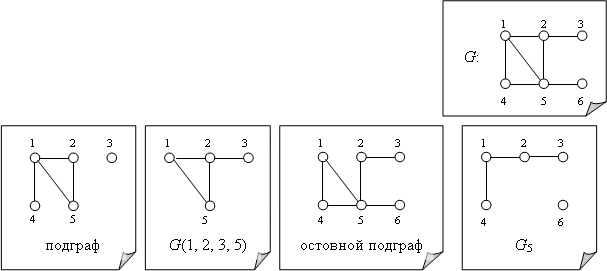
Другие переходы к подграфам или надграфом.
Дополнение графа. Граф ![]() называется дополнением графа G, если V(
называется дополнением графа G, если V(![]() ) = V(G), причём вершины U и V являются смежными в графе
) = V(G), причём вершины U и V являются смежными в графе ![]() тогда и только тогда, когда они не смежны в G. Таким образом, G и
тогда и только тогда, когда они не смежны в G. Таким образом, G и ![]() не имеют общих рёбер, а E(G) È E(
не имеют общих рёбер, а E(G) È E(![]() ) с общим множеством вершин образует полный граф.
) с общим множеством вершин образует полный граф.

Объединение графов.
Объединением графов G1 и G2 называется граф G1ÈG2, в котором V(G1ÈG2) = =V(G1)ÈV(G2) и E(G1ÈG2) = E(G1)ÈE(G2).
Пересечение графов.
Пересечением графов G1 и G2 называется граф G1ÇG2, в котором V(G1ÇG2) = =V(G1)ÇV(G2) и E(G1ÇG2) = E(G1)ÇE(G2).
 |
Соединение графов.
Соединением графов G1 и G2 называется объединение G1ÈG2, дополненное всеми рёбрами, соединяющими вершины G1 с вершинами G2. Обозначается соединение: G1+G2,
В частности, если Gi – (Ni, Mi)-графы, не имеющие общих вершин, то G1+G2 будет (N1+N2, M1+M2+N1×N2)-графом. Так, например, Kp,Q = 0P+ 0Q = ![]() +
+![]() .
.

Рассматриваются также другие более сложные операции на графах, такие как, произведение графов, прямое произведение и др.
| < Предыдущая | Следующая > |
|---|