3.01.2. Основные типы графов

Граф называется Пустым, если E(G) = Æ , т. е., если в нем нет ребер. Пустой граф порядка N обозначается 0N. Граф 01 называется Тривиальным. Граф, в котором любые две вершины соединены ребром называется Полным. Полный граф порядка N обозначается Kn.

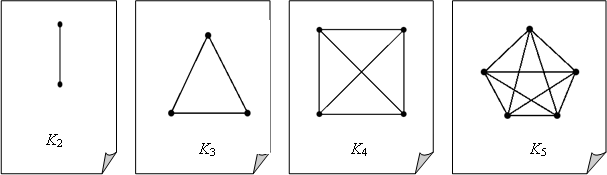Нетрудно подсчитать, что граф Kn им еет N(N-1)/2 ребер.

Граф такого вида, как на рис. 1, называется Простой цепью. Простая цепь порядка N обозначается Pn (на рисунке 1 изображена цепь P4). Простая цепь Pn Имеет N –1 ребер.

Замкнутые цепи, т. е. такие графы, как на рис. 2, называются Простыми циклами. Простой цикл порядка N обозначается Cn (на рис. 2 изображена простая цепь С7). Понятно, что простая цепь Cn имеет столько же ребер, сколько и вершин, т. е. N.

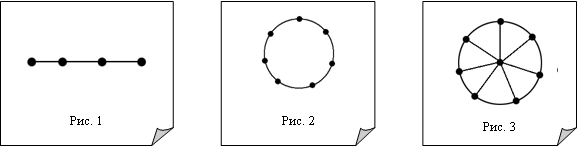Графы, такие как на рис. 3, называются колесами. Колесо порядка N+1 обозначается Wn (на рис. 3 изображено колесо W7); оно имеет 2N ребер.

Граф называется Двудольным, если множество его вершин можно разбить на два непустых подмножества (доли) так, что никакие две вершины одной доли не являются смежными. (Аналогично определяются трехдольные, четырехдольные и т. д. графы.) Таким образом, в двудольном графе смежными могут быть только вершины из разных долей (не обязательно каждая с каждой). Пример двудольного графа см. на рис. 4.

Если же в двудольном графе любые две вершины из разных долей соединены ребром, то такой граф называется Полным двудольным. Полный двудольный граф с N вершинами в одной доле и с M вершинами -- в другой обозначается Kn,M. См. примеры:

Графы K1,N называется Звездными графами, или Звездами.

Легко видеть, что граф Kn,M является (N+M, Nm)-Графом, т. е. имеет N+M вершин и Nm ребер.

Понятно, что существуют графы, которые можно одновременно отнести к нескольким типам. Например, K3 = C3, K2 = P2, K2, 2 = C4, K4 = W3.

< Предыдущая		Следующая >