1.3.5. Мощности бесконечных множеств. Счетные множества

Определение. Говорят, что множества А и В имеют одинаковую мощность (или, что они равномощны), если между А и В можно установить биекцию. Множества, равномощные множеству натуральных чисел, называются Счетными.

Установить биекцию с множеством натуральных чисел N фактически означает: сопоставить каждому элементу рассматриваемого множества номер, т. е. пронумеровать все элементы, или другими словами – пересчитать.

Конечное или счетное множество называется Не более чем счетным.

Примеры и свойства счетных множеств.

· Множество четных чисел 2N – счетное. Действительно, биекцию задает, например, отображение .

Задача гостинице “Бесконечность”.

В гостинице имеется счетное количество номеров, но все они заняты. Приехали еще 100 посетителей. Можно ли их разместить? А если приехали еще столько же, сколько уже имеется?

· Множество целых чисел Z счетно. Соответствующей биекцией, очевидно, является следующее отображение

· Объединение не более чем счетного множества счетных множеств – счетно.

Доказательство. Можно считать, что все множества и элементы в них уже пронумерованы. Пусть , , , … . Расположим все элементы объединения следующим образом и пронумеруем в порядке, указанном стрелкой:

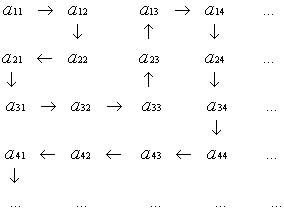
Понятно, что при указанном способе рассмотрения элементов всякий элемент рано или поздно получит свой номер. Если имеют непустые пересечения и в процессе нумерации встречаются элементы уже ранее пронумерованные, то их будем пропускать и переходить к следующим элементам.

· Прямое произведение конечного числа счетных множеств – счетно.

Доказательство. Пусть . Элементы декартового произведения расположим так же, как и в предыдущем примере (в виде бесконечной вправо и вниз прямоугольной таблицы) и пронумеруем аналогично. Таким образом, произведение двух счетных множеств --- счетно. Дальше по индукции для любого числа множителей.

· Множество Q -- рациональных чисел счетно.

Доказательство. Представим множество всех рациональных чисел в виде , где Q+ И Q - --- подмножества положительных и отрицательных рациональных чисел, соответственно. Достаточно показать, что Q+ Счетно. А это действительно так, поскольку

Есть объединение счетного количества счетных множеств.

· Множество алгебраических чисел A (корней всевозможных многочленов с целыми коэффициентами) – счетно (докажите).

< Предыдущая		Следующая >