1.3.2. Перестановки и размещения
Перестановкой из N Элементов называется всякий упорядоченный набор из данных элементов (всякое их расположение в определенном порядке). При изучении перестановок обычно интерес представляют не сами элементы, из которых перестановки состоят, а взаимное расположение этих элементов в перестановке. Поэтому отождествляя элементы с их номерами (можно считать, что рассматриваемые элементы пронумерованы), будем рассматривать перестановки чисел ![]() . Например, перестановками из 5 элементов будут
. Например, перестановками из 5 элементов будут ![]() ,
, ![]() ,
, ![]() ,
, ![]() и т. д. . Число различных перестановок из N элементов обозначается
и т. д. . Число различных перестановок из N элементов обозначается ![]() .
.
Теорема 1. ![]() , где
, где ![]() -- произведение всех натуральных чисел от 1 до N (читается: “эн-факториал”).
-- произведение всех натуральных чисел от 1 до N (читается: “эн-факториал”).
Доказательство. Действительно, чтобы получить подстановку нужно заполнить N позиций числами от 1 до N. На первую позицию можно поместить любое из N Чисел. Существует N Таких возможностей. После того, как первая позиция заполнена, на вторую позицию можно поместить любое число, кроме того, которое уже выбрано и стоит на первой позиции. Поэтому в распоряжении имеется ![]() возможностей. Всего количество способов заполнить первые две позиции равно
возможностей. Всего количество способов заполнить первые две позиции равно ![]() . Аналогично рассуждая дальше, находим, что для заполнения третьей позиции существует
. Аналогично рассуждая дальше, находим, что для заполнения третьей позиции существует ![]() возможности, и значит,
возможности, и значит, ![]() способов заполнить первые три позиции. Наконец, дойдя до последней N-ной позиции, на которую без альтернативы остается поместить последнее из оставшихся чисел, получим, что количество возможностей заполнить все позиции (и, значит, число различных подстановок из N элементов) равно
способов заполнить первые три позиции. Наконец, дойдя до последней N-ной позиции, на которую без альтернативы остается поместить последнее из оставшихся чисел, получим, что количество возможностей заполнить все позиции (и, значит, число различных подстановок из N элементов) равно ![]() , что и требовалось доказать.
, что и требовалось доказать.
Подчеркнем, что число ![]() с ростом N растет очень быстро. Так, например
с ростом N растет очень быстро. Так, например ![]() ,
, ![]() ,
, ![]() ,
, ![]() и т. д. . Для оценки
и т. д. . Для оценки ![]() при больших N применяется приближенная формула, которая называется формулой Стирлинга:
при больших N применяется приближенная формула, которая называется формулой Стирлинга:
 .
.
Размещением Из N Элементов по M называется всякий упорядоченный набор M элементов, выбранных из данных элементов. Точно так же, как в случае перестановок, можно считать, что элементами размещения являются натуральные числа. Например, размещениями из 5 элементов по 3 будут ![]() ,
, ![]() ,
, ![]() ,
, ![]() и т. д. . Перестановки также являются размещениями (из N Элементов по N). Число различных размещений из N элементов по M обозначается
и т. д. . Перестановки также являются размещениями (из N Элементов по N). Число различных размещений из N элементов по M обозначается ![]() . Рассуждая так же, как и при доказательстве теоремы 1, получим следующий результат.
. Рассуждая так же, как и при доказательстве теоремы 1, получим следующий результат.
Теорема 2. 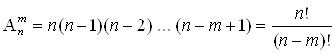 .
.
| < Предыдущая | Следующая > |
|---|