Лекция 13. Сети. Пути в орграфах. Остовы минимальной длины
Определение. Двуполюсной сетью называется связный граф без петель с двумя выделенными вершинами, которые называются полюсами.
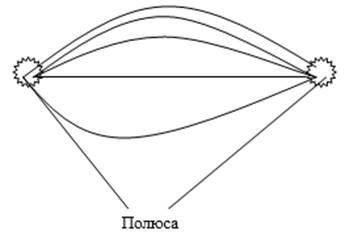
Двуполюсная сеть называется сильно связанной (связной), если через любое ребро проходит простая цепь, соединяющая полюса. В ней нет повторяющихся вершин.
Параллельная сеть – сеть вида
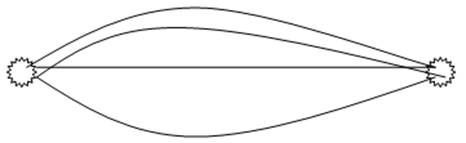
Последовательная сеть – сеть вида

П (пи) сети – последовательно-параллельные сети
Примеры П-сетей
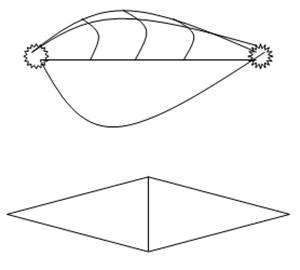
Такая сеть называется мостиковой.
Контактными схемами называются сильносвязные двуполюсные сети, каждому ребру которой поставлено в соответствие x или NOT(x).
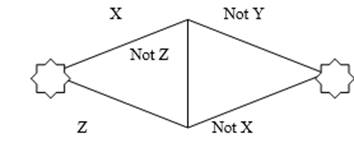
Любой контактной схеме (КС) можно поставить в соответствие булеву функцию (функцию проводимости) по правилу:
Для любой простой цепи, соединяющей полюса, записываем ЭК тех переменных, которыми помечены ребра этой цепи.
Затем берем дизъюнкцию всех ЭК. Получим искомую функцию проводимости.
Если в контактной схеме будут стоять переключатели (релейные контакты), которые будем считать замкнутыми, если выражение, стоящее у ребра равно 1 или в противном случае разомкнутыми, то при подаче на полюса разности потенциалов (электрического тока) контактная схема будет проводить ток при таких и только при таких состояниях контактов, при которых значение функции равно 1.
Минимальной контактной схемой для функции называется контактная схема, для которой эта функция является функцией проводимости. Эта схема содержит наименьшее число ребер.
Чтобы построить минимальную КС, надо выписать минимальную ДНФ для данной функции, упростить путем вынесения за скобки, нарисовать П-сеть, реализующую КС для функции и постараться найти мостиковые соединения.
Минимальные пути в графах
Путем в графе (в орграфе) называется маршрут, движение по которому любого ребра проходит в соответствии с направлением этого ребра.
Контуром в орграфе называется замкнутый путь, в котором вершины не повторяются (кроме первой и последней).
Орграф, в котором нет ни одного контура, называется бесконтурным.
Первая задача о минимальном пути.
Дан граф. Выделено две вершины. Найти путь из одной вершины в другую, состоящий из наименьшего числа ребер.
Введем обозначения
Г(V) – множество вершин, в которые можно попасть из вершины V, пройдя только по одному ребру в его направлении.
Г-1(V) – множество вершин, из которых можно попасть в вершину V, пройдя только по одному ребру.
Алгоритм.
1. Исходной вершине A присваиваем метку 0.
2. Любому Г(А), которые еще не имели меток, присваиваем метку М = 1.
3. Для любой V, принадлежащей Г(А) находим Г(V) и любой V, принадлежащему Г(V), если она не имела метку, даем метку 2.
4. И так далее до тех пор, пока конечная вершина не получит метку.
5. Выбираем путь по Г-1(V).
Может произойти такое, что пути из А в В нет вообще.
Тогда на некотором шаге при обратном ходе нужной вершины нет.
Вторая задача.
Если каждому ребру поставить в соответствие некоторое целое положительное число, называемое его длиной и требуется найти путь из А в В, такой, что ![]() I = minimum. (r или l – длина ребра)
I = minimum. (r или l – длина ребра)
Алгоритм будет следующий.
1. Метка для ребра А l1 = 0
Для Vi li = +(бесконечность) – очень большое число, большее суммы всех длин ребер всего графа.
L(Vi, Vj) – длина ребра, идущего из вершины Vi в Vj. Направление важно.
2. Для любого ребра из графа проверяем выполнение неравенства.
Lj - li > L(Vi, Vj) *
Если это неравенство выполняется, то меняем метку lj на новую.
Lj = li + L(Vi, Vj) и так до тех пор, пока выполняется *.
Если * нигде не выполняется, то та метка, которая будет стоять у вершины В и будет равна длине минимального пути из А в В, а сам путь строится движением назад из В в А.
Г-1(В) Существует такое ребро Vi1, для которого выполнено равенство.
Lb - li1 = L(Vi1,B)
Затем Г-1(V1) Существует V2, где l(V1) - l(V2) = L(V1, V2) и т. д. пока не вернемся в вершину А.
Путь минимальной длины найден.
Остов графа минимальной длины.
Остов – дерево, содержащее все вершины графа и какие-то из его ребер.
Если каждому ребру графа поставлена в соответствие его длина, то требуется найти такой остов, сумма длин ребер которого минимальна.
Алгоритм
1. Перенумеруем все ребра графа в порядке возрастания их длин.
2. Просматриваем ребра, начиная с первого. Если x1 не является петлей, мы его включаем в остов и переходим к следующему ребру. Если оно не является петлей и не образует с уже имеющимися ребрами цикла, мы его включаем в остов. И так до тех пор, пока не рассмотрим все ребра.
Остов минимальной длины найден.
| < Предыдущая | Следующая > |
|---|