01. Геометрия гладких многообразий
Пусть ![]() – гладкое
– гладкое ![]() -мерное многообразие и
-мерное многообразие и ![]() – произвольная точка в нем. Говорят, что на многообразии
– произвольная точка в нем. Говорят, что на многообразии ![]() дана Кривая, если имеется непрерывное отображение
дана Кривая, если имеется непрерывное отображение ![]() интервала
интервала ![]() в
в ![]() Пусть
Пусть ![]() – локальные координаты в окрестности точки
– локальные координаты в окрестности точки ![]() . Тогда кривая
. Тогда кривая ![]() в локальных координатах может быть записана в виде
в локальных координатах может быть записана в виде ![]() . Кривая называется Гладкой, если все функции
. Кривая называется Гладкой, если все функции ![]() , определяющие эту кривую, гладкие. Пусть кривая
, определяющие эту кривую, гладкие. Пусть кривая ![]() проходит через точку
проходит через точку ![]() , мы можем считать, что
, мы можем считать, что ![]() .
.
Касательным вектором к кривой ![]() в точке
в точке ![]() называется вектор
называется вектор ![]() .
.
Пример 1. Отображение ![]() , заданное следующим образом
, заданное следующим образом 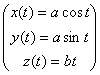
Называется винтовой линией в ![]() . Очевидно, что это гладкая кривая и касательный вектор к ней в точке
. Очевидно, что это гладкая кривая и касательный вектор к ней в точке ![]() есть
есть  .
.
Отметим, что выражение касательного вектора в данной точке зависит от координатной карты. Действительно, пусть ![]() – другие локальные координаты в окрестности точки
– другие локальные координаты в окрестности точки ![]() . Тогда при переходе от карты
. Тогда при переходе от карты ![]() к карте
к карте ![]() координаты вектора преобразуются по закону
координаты вектора преобразуются по закону ![]() , который легко следует из правила дифференцирования сложной функции.
, который легко следует из правила дифференцирования сложной функции.
Различным кривым, проходящим через точку ![]() , соответствуют, вообще говоря, различные касательные векторы. Но возможна также ситуация, когда две различные кривые в общей точке имеют одинаковые касательные векторы, например винтовая линия из примера 1 и прямая
, соответствуют, вообще говоря, различные касательные векторы. Но возможна также ситуация, когда две различные кривые в общей точке имеют одинаковые касательные векторы, например винтовая линия из примера 1 и прямая  в общей точке
в общей точке ![]() имеют одинаковые касательные векторы
имеют одинаковые касательные векторы ![]() .
.
Все касательные векторы многообразия ![]() в точке
в точке ![]() образуют векторное пространство, которое называется Касательным пространством к
образуют векторное пространство, которое называется Касательным пространством к ![]() в точке
в точке ![]() и обозначается
и обозначается ![]() . Размерность касательного пространства
. Размерность касательного пространства ![]() равна размерности гладкого многообразия
равна размерности гладкого многообразия ![]() .
.
Мы можем рассмотреть следующую ![]() -ю координатную кривую в многообразии
-ю координатную кривую в многообразии ![]() :
: ![]() и через
и через ![]() обозначить ее касательный вектор
обозначить ее касательный вектор ![]() в точке
в точке ![]() . Тогда векторы
. Тогда векторы ![]() образуют базис касательного пространства
образуют базис касательного пространства ![]() в точке
в точке ![]() .
.
Любой вектор ![]() на многообразии можно рассматривать как Дифференциальный оператор, действующий на гладких функциях. Вектор
на многообразии можно рассматривать как Дифференциальный оператор, действующий на гладких функциях. Вектор ![]() переводит функцию
переводит функцию ![]() в число
в число ![]() . Производные вычисляются в той точке, где задан касательный вектор
. Производные вычисляются в той точке, где задан касательный вектор ![]() . Это определение не зависит от выбора карты. Действительно,
. Это определение не зависит от выбора карты. Действительно, ![]() . Здесь мы используем следующее сокращенное правило суммирования : если в некотором выражении индекс входит дважды, один раз как верхний, а другой раз как нижний, то по нему подразумевается суммирование.
. Здесь мы используем следующее сокращенное правило суммирования : если в некотором выражении индекс входит дважды, один раз как верхний, а другой раз как нижний, то по нему подразумевается суммирование.
Лемма. Если дифференциальный оператор ![]() Инвариантен относительно выбора карты, то его коэффициенты
Инвариантен относительно выбора карты, то его коэффициенты ![]() Образуют вектор.
Образуют вектор.
Доказательство. Из равенства ![]() следует, что
следует, что ![]() . Отсюда следует, что
. Отсюда следует, что ![]() , так как предыдущее равенство имеет место для любой функции
, так как предыдущее равенство имеет место для любой функции ![]() .
.
Итак, векторы из ![]() находятся во взаимно однозначном соответствии с инвариантными операторами вида
находятся во взаимно однозначном соответствии с инвариантными операторами вида ![]() .
.
Говорят, что на многообразии ![]() задано Векторное поле
задано Векторное поле ![]() , если в каждой его точке
, если в каждой его точке ![]() задан вектор
задан вектор![]() . В локальных координатах векторное поле задается в виде
. В локальных координатах векторное поле задается в виде ![]() , Векторное поле называется Гладким, если все функции
, Векторное поле называется Гладким, если все функции ![]() являются гладкими.
являются гладкими.
Траекторией ![]() данного векторного поля
данного векторного поля ![]() называется такая кривая
называется такая кривая![]() , что
, что ![]() . Из общей теории обыкновенных дифференциальных уравнений следует, что найдется такое
. Из общей теории обыкновенных дифференциальных уравнений следует, что найдется такое ![]() , что на интервале
, что на интервале ![]() всегда существует траектория векторного поля
всегда существует траектория векторного поля ![]() . Каждая данная траектория может быть единственным образом продолжена на некоторый максимальный интервал
. Каждая данная траектория может быть единственным образом продолжена на некоторый максимальный интервал ![]() . Если
. Если ![]() , то траектория называется Полной. Точка
, то траектория называется Полной. Точка ![]() , в которой все координаты векторного поля обращаются в нуль
, в которой все координаты векторного поля обращаются в нуль ![]() , называется Особой точкой векторного поля.
, называется Особой точкой векторного поля.
Пример. Рассмотрим на единичной сфере ![]() векторное поле
векторное поле ![]() . Очевидно, что его траекториями будет семейство параллелей
. Очевидно, что его траекториями будет семейство параллелей ![]() . Все траектории полные. У данного поля две особые точки:
. Все траектории полные. У данного поля две особые точки: ![]() и
и ![]() . Из топологических соображений на двумерной сфере не существует гладкого векторного поля без особых точек.
. Из топологических соображений на двумерной сфере не существует гладкого векторного поля без особых точек.
Пусть ![]() – отображение класса
– отображение класса ![]() двух гладких многообразий. Для точки
двух гладких многообразий. Для точки ![]() определим линейное отображение
определим линейное отображение ![]() следующим образом : пусть вектор
следующим образом : пусть вектор ![]() , где
, где ![]() – некоторая кривая в
– некоторая кривая в ![]() , проходящая через точку
, проходящая через точку ![]() , тогда
, тогда ![]() есть кривая в
есть кривая в ![]() , проходящая через точку
, проходящая через точку ![]() . Положим
. Положим ![]() . Данное линейное отображение касательных пространств называется Дифференциалом гладкого отображения
. Данное линейное отображение касательных пространств называется Дифференциалом гладкого отображения ![]() в точке
в точке ![]() и обозначается
и обозначается ![]() или
или ![]() .
.
В локальных координатах ![]() на многообразии
на многообразии ![]() дифференциал задается с помощью матрицы Якоби следующим образом:
дифференциал задается с помощью матрицы Якоби следующим образом: 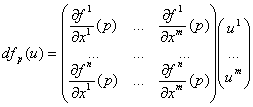
Дифференциал отображения ![]() обладает следующим свойством.
обладает следующим свойством.
Лемма. Имеет место равенство ![]() , где
, где ![]() и
и ![]() .
.
Доказательство.
 ,ч. т.д.
,ч. т.д.
Пример. Рассмотрим так называемые географические координаты на сфере ![]() . Пусть
. Пусть ![]() и задано отображение
и задано отображение ![]() следующим образом:
следующим образом: 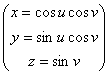 . Тогда дифференциал этого отображения в точке
. Тогда дифференциал этого отображения в точке ![]() имеет вид
имеет вид ![]()
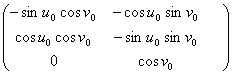 . При этом дифференциал отображает касательный вектор
. При этом дифференциал отображает касательный вектор ![]() в вектор
в вектор  , а вектор
, а вектор ![]() в вектор
в вектор 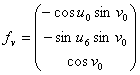 . Вектор
. Вектор ![]() касателен к параллелям на сфере, а вектор
касателен к параллелям на сфере, а вектор ![]() – к меридианам.
– к меридианам.
Теперь мы изучим геометрию ортогональной группы матриц. Напомним, что квадратная матрица ![]() размера
размера ![]() с вещественными элементами называется Ортогональной, если
с вещественными элементами называется Ортогональной, если ![]() . Множество всех ортогональных матриц образует группу, обозначаемую
. Множество всех ортогональных матриц образует группу, обозначаемую ![]() .
.
Группа ![]() вложена в пространство
вложена в пространство ![]() , поскольку любую матрицу можно записать в строку длины
, поскольку любую матрицу можно записать в строку длины ![]() . Соотношение
. Соотношение ![]() равносильно системе из
равносильно системе из ![]() уравнений. Пусть
уравнений. Пусть ![]() и рассмотрим отображение
и рассмотрим отображение ![]() по формуле
по формуле ![]() . Ясно, что в нулевую матрицу при данном отображении переводятся ортогональные матрицы, следовательно
. Ясно, что в нулевую матрицу при данном отображении переводятся ортогональные матрицы, следовательно ![]() . Вычислим дифференциал отображения
. Вычислим дифференциал отображения ![]() .
.
Для этого рассмотрим кривую ![]() , такую что
, такую что ![]() и
и ![]() – данная матрица. Имеем
– данная матрица. Имеем ![]() Очевидно, что
Очевидно, что ![]() – симметрическая матрица. Любая симметрическая матрица представима в виде
– симметрическая матрица. Любая симметрическая матрица представима в виде ![]() где
где ![]() для некоторой матрицы
для некоторой матрицы ![]() . Достаточно положить
. Достаточно положить ![]() . Итак, образ
. Итак, образ ![]() отображения
отображения ![]() совпадает с пространством симметрических матриц, следовательно, ранг матрицы Якоби системы, описывающей группу
совпадает с пространством симметрических матриц, следовательно, ранг матрицы Якоби системы, описывающей группу ![]() – постоянен. По теореме о неявной функции множество
– постоянен. По теореме о неявной функции множество ![]() представляет собой гладкое многообразие. Вычислим размерность этого многообразия. Имеем
представляет собой гладкое многообразие. Вычислим размерность этого многообразия. Имеем ![]() {пространства симметрических матриц}=
{пространства симметрических матриц}=![]() . Поэтому
. Поэтому ![]() . В частности, размерность группы
. В частности, размерность группы ![]() являющейся связной компонентой единицы группы
являющейся связной компонентой единицы группы ![]() , равна 3.
, равна 3.
Литература. 1. Трофимов В. В. гл.1 , параграфы 8,9.
2. Бишоп Р. Л., Криттенден Р. Дж. гл.1, 1.3,1.4.
| Следующая > |
|---|