83. Основные теоремы о пределах

Теорема 1. , где С = const.

Следующие теоремы справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при х®а.

Теорема 2.

Доказательство этой теоремы будет приведено ниже.

Теорема 3.

Следствие.

Теорема 4. 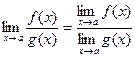при

Теорема 5. Если F(X)>0 вблизи точки х = а и , то А>0.

Аналогично определяется знак предела при f(x) < 0, f(x) ³ 0, f(x) £ 0.

Теорема 6. Если G(X) £ F(X) £ U(X) вблизи точки х = а и , то и .

ОПределение. Функция f(x) называется Ограниченной Вблизи точки х = а, если существует такое число М>0, что ïf(x)ï<M вблизи точки х = а.

Теорема 7. Если функция F(X) имеет конечный предел при х®А, то она ограничена вблизи точки х = а.

Доказательство. Пусть , т. е. , тогда

или

, т. е.

Где М = e + ïАï

Теорема доказана.

< Предыдущая		Следующая >