75. Квадратичные формы

Определение: Однородный многочлен второй степени относительно переменных Х1 И Х2

Ф(х1, х2) = а11

Не содержащий свободного члена и неизвестных в первой степени называется Квадратичной формой переменных Х1 и Х2.

Определение: Однородный многочлен второй степени относительно переменных Х1, Х2 и Х3

Не содержащий свободного члена и неизвестных в первой степени называется Квадратичной формой переменных Х1, Х2 и Х3.

Рассмотрим квадратичную форму двух переменных. Квадратичная форма имеет симметрическую матрицу А = 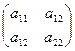. Определитель этой матрицы называется Определителем квадратичной формы.

Пусть на плоскости задан ортогональный базис . Каждая точка плоскости имеет в этом базисе координаты х1, х2.

Если задана квадратичная форма Ф(х1, х2) = а11, то ее можно рассматривать как функцию от переменных х1 и х2.

< Предыдущая		Следующая >