57. Общие уравнения прямой в пространстве

Уравнение прямой может быть рассмотрено как уравнение линии пересечения двух плоскостей.

Как было рассмотрено выше, плоскость в векторной форме может быть задана уравнением:

×+ D = 0, где

- нормаль плоскости; - радиус - вектор произвольной точки плоскости.

Пусть в пространстве заданы две плоскости: ×+ D1 = 0 и ×+ D2 = 0, векторы нормали имеют координаты: (A1, B1, C1), (A2, B2, C2); (x, y, z).

Тогда общие уравнения прямой в векторной форме:

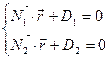
Общие уравнения прямой в координатной форме:

Практическая задача часто состоит в приведении уравнений прямых в общем виде к каноническому виду.

Для этого надо найти произвольную точку прямой и числа m, n, p.

При этом направляющий вектор прямой может быть найден как векторное произведение векторов нормали к заданным плоскостям.

Пример. Найти каноническое уравнение, если прямая задана в виде:

Для нахождения произвольной точки прямой, примем ее координату х = 0, а затем подставим это значение в заданную систему уравнений.

, т. е. А(0, 2, 1).

Находим компоненты направляющего вектора прямой.

Тогда канонические уравнения прямой:

Пример. Привести к каноническому виду уравнение прямой, заданное в виде:

Для нахождения произвольной точки прямой, являющейся линией пересечения указанных выше плоскостей, примем z = 0. Тогда:

;

2x – 9x – 7 = 0;

X = -1; y = 3;

Получаем: A(-1; 3; 0).

Направляющий вектор прямой: .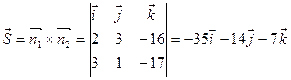

Итого:

< Предыдущая		Следующая >