55. Уравнение прямой в пространстве по точке и направляющему вектору
Возьмем произвольную прямую и вектор ![]() (m, n, p), параллельный данной прямой. Вектор
(m, n, p), параллельный данной прямой. Вектор ![]() Называется Направляющим вектором прямой.
Называется Направляющим вектором прямой.
На прямой возьмем две произвольные точки М0(x0, y0, z0) и M(x, y, z).
 z
z
![]() M1
M1
M0
![]()
![]()
0 y
x
Обозначим радиус - векторы этих точек как ![]() И
И ![]() , очевидно, что
, очевидно, что ![]() -
- ![]() =
= ![]() .
.
Т. к. векторы ![]() И
И ![]() коллинеарны, то верно соотношение
коллинеарны, то верно соотношение ![]() =
= ![]() T, где t – некоторый параметр.
T, где t – некоторый параметр.
Итого, можно записать: ![]() =
= ![]() +
+ ![]() T.
T.
Т. к. этому уравнению удовлетворяют координаты любой точки прямой, то полученное уравнение – Параметрическое уравнение прямой.
Это векторное уравнение может быть представлено в координатной форме:
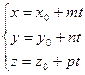
Преобразовав эту систему и приравняв значения параметра t, получаем канонические уравнения прямой в пространстве:
![]() .
.
Определение. Направляющими косинусами Прямой называются направляющие косинусы вектора ![]() , которые могут быть вычислены по формулам:
, которые могут быть вычислены по формулам:
![]() ;
; ![]()
![]() .
.
Отсюда получим: m : n : p = cosa : cosb : cosg.
Числа m, n, p называются Угловыми коэффициентами прямой. Т. к. ![]() - ненулевой вектор, то m, n и p не могут равняться нулю одновременно, но одно или два из этих чисел могут равняться нулю. В этом случае в уравнении прямой следует приравнять нулю соответствующие числители.
- ненулевой вектор, то m, n и p не могут равняться нулю одновременно, но одно или два из этих чисел могут равняться нулю. В этом случае в уравнении прямой следует приравнять нулю соответствующие числители.
| < Предыдущая | Следующая > |
|---|