51. Парабола

Определение. Параболой называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.

Расположим начало координат посередине между фокусом и директрисой.

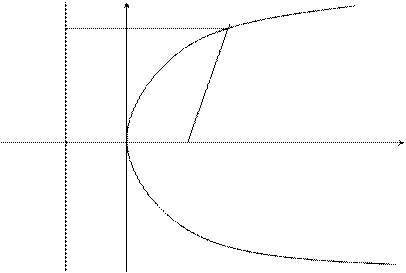у

А М(х, у)

О F x

p/2 p/2

Величина р (расстояние от фокуса до директрисы) называется Параметром Параболы. Выведем каноническое уравнение параболы.

Из геометрических соотношений: AM = MF; AM = x + p/2;

MF2 = y2 + (x – p/2)2

(x + p/2)2 = y2 + (x – p/2)2

X2 +xp + p2/4 = y2 + x2 – xp + p2/4

Y2 = 2px

Уравнение директрисы: x = - p/2.

Пример. На параболе у2 = 8х найти точку, расстояние которой от директрисы равно 4.

Из уравнения параболы получаем, что р = 4.

R = x + p/2 = 4; следовательно:

X = 2; y2 = 16; y = ±4. Искомые точки: M1(2; 4), M2(2; -4).

< Предыдущая		Следующая >