49. Эллипс
Определение. Эллипсом называется линия, заданная уравнением ![]() .
.
ОПределение. Фокусами Называются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.
 у
у
М
R1
r2
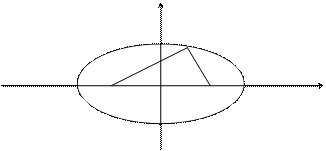
F1 O F2 х
F1, F2 – фокусы. F1 = (c; 0); F2(-c; 0)
С – половина расстояния между фокусами;
A – большая полуось;
B – малая полуось.
Теорема. Фокусное расстояние и полуоси эллипса связаны соотношением:
A2 = B2 + C2.
Доказательство: В случае, если точка М находится на пересечении эллипса с вертикальной осью, R1 + R2 = 2![]() (по теореме Пифагора). В случае, если точка М находится на пересечении эллипса с горизонтальной осью, R1 + R2 = A – C + A + C. Т. к. по определению сумма R1 + R2 – постоянная величина, то, приравнивая, получаем:
(по теореме Пифагора). В случае, если точка М находится на пересечении эллипса с горизонтальной осью, R1 + R2 = A – C + A + C. Т. к. по определению сумма R1 + R2 – постоянная величина, то, приравнивая, получаем:
A2 = B2 + C2
R1 + R2 = 2A.
Определение. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется Эксцентриситетом.
Е = с/a.
Т. к. с < a, то е < 1.
Определение. Величина k = b/a называется Коэффициентом сжатия Эллипса, а величина 1 – k = (a – b)/a называется Сжатием Эллипса.
Коэффициент сжатия и эксцентриситет связаны соотношением: k2 = 1 – e2.
Если a = b (c = 0, e = 0, фокусы сливаются), то эллипс превращается в окружность.
Если для точки М(х1, у1) выполняется условие: ![]() , то она находится внутри эллипса, а если
, то она находится внутри эллипса, а если ![]() , то точка находится вне эллипса.
, то точка находится вне эллипса.
Теорема. Для произвольной точки М(х, у), принадлежащей эллипсу верны соотношения:
R1 = a – ex, r2 = a + ex.
Доказательство. Выше было показано, что r1 + r2 = 2a. Кроме того, из геометрических соображений можно записать:
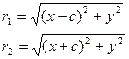
![]()
После возведения в квадрат и приведения подобных слагаемых:
![]()
![]()
![]()
Аналогично доказывается, что r2 = a + ex. Теорема доказана.
С эллипсом связаны две прямые, называемые Директрисами. Их уравнения:
X = a/e; x = - a/e.
Теорема. Для того, чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету е.
Пример. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса, заданного уравнением: ![]()
1) Координаты нижней вершины: x = 0; y2 = 16; y = -4.
2) Координаты левого фокуса: c2 = a2 – b2 = 25 – 16 = 9; c = 3; F2(-3; 0).
3) Уравнение прямой, проходящей через две точки:
![]()
Пример. Составить уравнение эллипса, если его фокусы F1(0; 0), F2(1; 1), большая ось равна 2.
Уравнение эллипса имеет вид: ![]() . Расстояние между фокусами:
. Расстояние между фокусами:
2c = ![]() , таким образом, a2 – b2 = c2 = ½
, таким образом, a2 – b2 = c2 = ½
По условию 2а = 2, следовательно а = 1, b = ![]()
Итого: ![]() .
.
| < Предыдущая | Следующая > |
|---|