43. Нормальное уравнение прямой

Если обе части уравнения Ах + Ву + С = 0 разделить на число , которое называется Нормирующем множителем, то получим

Xcosj + ysinj - p = 0 –

Нормальное уравнение прямой.

Знак ± нормирующего множителя надо выбирать так, чтобы m×С < 0.

Р – длина перпендикуляра, опущенного из начала координат на прямую, а j - угол, образованный этим перпендикуляром с положительным направлением оси Ох.

Пример. Дано общее уравнение прямой 12х – 5у – 65 = 0. Требуется написать различные типы уравнений этой прямой.

Уравнение этой прямой в отрезках: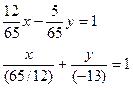

Уравнение этой прямой с угловым коэффициентом: (делим на 5)

Нормальное уравнение прямой:

; cosj = 12/13; sinj = -5/13; p = 5.

Cледует отметить, что не каждую прямую можно представить уравнением в отрезках, например, прямые, параллельные осям или проходящие через начало координат.

Пример. Прямая отсекает на координатных осях равные положительные отрезки. Составить уравнение прямой, если площадь треугольника, образованного этими отрезками равна 8 см2.

Уравнение прямой имеет вид: , a = b = 1; ab/2 = 8; a = 4; -4.

A = -4 не подходит по условию задачи.

Итого: или х + у – 4 = 0.

Пример. Составить уравнение прямой, проходящей через точку А(-2, -3) и начало координат.

Уравнение прямой имеет вид: , где х1 = у1 = 0; x2 = -2; y2 = -3.

Для самостоятельного решения: Составить уравнения прямых, проходящих через точку М(-3, -4) и параллельных осям координат.

Ответ: { x + 3 = 0; y + 4 = 0}.

< Предыдущая		Следующая >