30. Уравнение плоскости, проходящей через три точки

Для того, чтобы через три какие - либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.

Рассмотрим точки М1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3) в общей декартовой системе координат.

Для того, чтобы произвольная точка М(x, y, z) лежала в одной плоскости с точками М1, М2, М3 необходимо, чтобы векторы были компланарны.

() = 0

Таким образом,

Уравнение плоскости, проходящей через три точки:

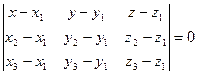
< Предыдущая		Следующая >