26. Свойства векторного произведения векторов
1) ![]() ;
;
2) ![]() , если
, если ![]() ïï
ïï![]() или
или ![]() = 0 или
= 0 или ![]() = 0;
= 0;
3) (m![]() )´
)´![]() =
= ![]() ´(m
´(m![]() ) = m(
) = m(![]() ´
´![]() );
);
4) ![]() ´(
´(![]() +
+ ![]() ) =
) = ![]() ´
´![]() +
+ ![]() ´
´ ![]() ;
;
5) Если заданы векторы ![]() (Xa, Ya, Za) и
(Xa, Ya, Za) и ![]() (Xb, Yb, Zb) в декартовой прямоугольной системе координат с единичными векторами
(Xb, Yb, Zb) в декартовой прямоугольной системе координат с единичными векторами ![]() , то
, то
![]() ´
´![]() =
=
6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах ![]() И
И ![]() .
.
Пример. Найти векторное произведение векторов ![]() И
И
![]() .
.
![]() = (2, 5, 1);
= (2, 5, 1); ![]() = (1, 2, -3)
= (1, 2, -3)
 .
.
При использовании компьютерной версии “Курса высшей математики” можно запустить программу, которая может найти скалярное и векторное произведения двух векторов. Для запуска программы дважды щелкните на значке:
 |
В открывшемся окне программы введите координаты векторов и нажмите Enter. После получения скалярного произведения нажмите Enter еще раз – будет получено векторное произведение.
Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (Ó Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.
Пример. Вычислить площадь треугольника с вершинами А(2, 2, 2), В(4, 0, 3),
С(0, 1, 0).

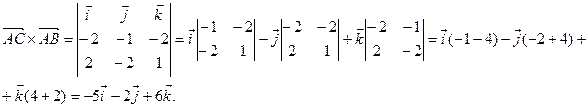
![]()
![]() (ед2).
(ед2).
Пример. Доказать, что векторы ![]() ,
, ![]() И
И ![]() компланарны.
компланарны.
 , т. к. векторы линейно зависимы, то они компланарны.
, т. к. векторы линейно зависимы, то они компланарны.
Пример. Найти площадь параллелограмма, построенного на векторах ![]() , если
, если ![]()
![]()
![]() (ед2).
(ед2).
| < Предыдущая | Следующая > |
|---|