22. Декартова система координат

Зафиксируем в пространстве точку О и рассмотрим произвольную точку М.

Вектор назовем радиус - вектором точки М. Если в пространстве задать некоторый базис, то точке М можно сопоставить некоторую тройку чисел – компоненты ее радиус - вектора.

Определение. Декартовой системой координат в пространстве называется совокупность точки и базиса. Точка называется Началом координат. Прямые, проходящие через начало координат называются Осями координат.

1-я ось – ось Абсцисс

2-я ось – ось Ординат

3-я ось – ось Апликат

Чтобы найти компоненты вектора нужно из координат его конца вычесть координаты начала.

Если заданы точки А(x1, y1, z1), B(x2, y2, z2), то = (x2 – x1, y2 – y1, z2 – z1).

Определение. Базис называется Ортонормированным, если его векторы попарно ортогональны и равны единице.

Определение. Декартова система координат, базис которой ортонормирован называется Декартовой прямоугольной системой координат.

Пример. Даны векторы(1; 2; 3), (-1; 0; 3), (2; 1; -1) и (3; 2; 2) в некотором базисе. Показать, что векторы , и Образуют базис и найти координаты вектора в этом базисе.

Векторы образуют базис, если они линейно независимы, другими словами, если уравнения, входящие в систему:

линейно независимы.

Тогда .

Это условие выполняется, если определитель матрицы системы отличен от нуля.

Для решения этой системы воспользуемся методом Крамера.

D1 =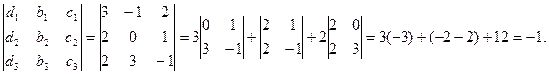

;

D2 =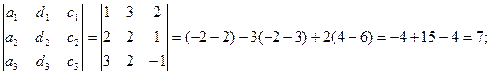

D3 =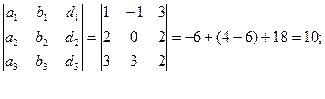

Итого, координаты вектора В базисе , , : { -1/4, 7/4, 5/2}.

При использовании компьютерной версии “Курса высшей математики” можно запустить программу, которая позволит разложить любой вектор по любому новому базису, т. е. решить предыдущий пример для любых векторов , , , .

Для запуска программы дважды щелкните по значку:

В открывшемся окне программы введите координаты векторов и нажмите Enter.

Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (Ó Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.

Длина вектора в координатах определяется как расстояние между точками начала и конца вектора. Если заданы две точки в пространстве А(х1, y1, z1), B(x2, y2, z2), то .

Если точка М(х, у, z) Делит отрезок АВ в соотношении L/M, то координаты этой точки определяются как:

В частном случае координаты Середины отрезка находятся как:

X = (x1 + x2)/2; y = (y1 + y2)/2; z = (z1 + z2)/2.

< Предыдущая		Следующая >