17. Метод Гаусса

(Карл Фридрих Гаусс (1777-1855) немецкий математик)

В отличие от Матричного метода и Метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.

Рассмотрим систему линейных уравнений:

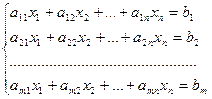
Разделим обе части 1–го уравнения на a11 ¹ 0, затем:

1) умножим на а21 и вычтем из второго уравнения

2) умножим на а31 и вычтем из третьего уравнения

и т. д.

Получим:

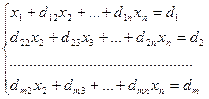, где D1j = a1j/a11, j = 2, 3, …, n+1.

Dij = aij – ai1d1j i = 2, 3, … , n; j = 2, 3, … , n+1.

Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т. д.

Пример. Решить систему линейных уравнений методом Гаусса.

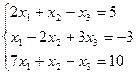
Составим расширенную матрицу системы.

А* =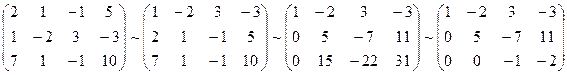

Таким образом, исходная система может быть представлена в виде:

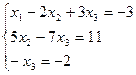, откуда получаем: x3 = 2; x2 = 5; x1 = 1.

Пример. Решить систему методом Гаусса.

Составим расширенную матрицу системы.

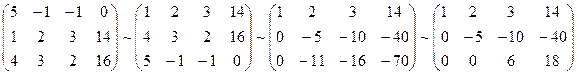
Таким образом, исходная система может быть представлена в виде:

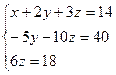, откуда получаем: z = 3; y = 2; x = 1.

Полученный ответ совпадает с ответом, полученным для данной системы методом Крамера и матричным методом.

Для самостоятельного решения:

Ответ: {1, 2, 3, 4}.

При использовании компьютерной версии “Курса высшей математики” можно запустить программу, которая решит любую систему линейных уравнений 3- го порядка методом Крамера и методом Гаусса или систему 4 – го порядка методом Гаусса. Достаточно ввести только коэффициенты при переменных системы. Программа выдаст подробный отчет о ходе решения и результатах.

Для запуска программы дважды щелкните на значке:

В открывшемся окне выберите необходимый метод решения и следуйте имеющимся в программе указаниям.

Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (Ó Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.

< Предыдущая		Следующая >