_114. Эйлеровы и гамильтоновы графы

Определение. Цепь (цикл) в псевдографе G называется Эйлеровым, если она проходит по одному разу через каждое ребро псевдографа G.

Теорема. Для того, чтобы связный псевдограф G Обладал эйлеровым циклом, необходимо и достаточно, чтобы степени его вершин были четными.

Теорема. Для того, чтобы связный псевдограф G Обладал эйлеровой цепью, необходимо и достаточно, чтобы он имел ровно две вершины нечетной степени.

Определение. Цикл (цепь) в псевдографе G называется Гамильтоновым, если он проходит через каждую вершину псевдографа G ровно один раз.

Пример.

- в графе есть и эйлеровый и гамильтонов циклы

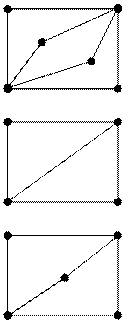- в графе есть эйлеров цикл, но нет гамильтонова

- в графе есть гамильтонов, но нет эйлерова цикла

- в графе нет ни эйлерова, ни гамильтонова цикла

Граф G называется Полным, если если каждая его вершина смежна со всеми остальными вершинами. В полном графе всегда существуют гамильтоновы цмклы.

Также необходимым условием существования гамильтонова цикла явояется связность графа.

< Предыдущая		Следующая >