_112. Матрицы графов
Пусть D = (V, X) – орграф, где V = {v1, …, vn}, X = {x1, … , xm}.
Определение. Матрицей смежности орграфа D называется квадратичная матрица A(D) = [aij] порядка П, у которой
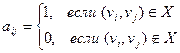
Определение. Если вершина V является крнцом ребра Х, то говорят, что V и Х – инциндентны.
Определение. Матрицей инциндентности оргафа D называется матрица размерности П´Т B(D) = [bij], у которой
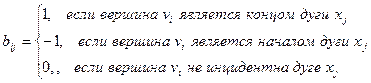
Пример. Записать матрицы смежности и инцидентности для графа, изображенного на рисунке.
X1
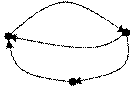
V1 X4 V2
X2
X3
V3
Составим матрицу смежности:
|
V1 |
V2 |
V3 |
|
|
V1 |
0 |
1 |
0 |
|
V2 |
1 |
0 |
1 |
|
V3 |
1 |
0 |
0 |
Т. е. 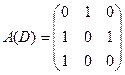 - матрица смежности.
- матрица смежности.
Матрица инциндентности:
|
X1 |
X2 |
X3 |
X4 |
|
|
V1 |
-1 |
0 |
1 |
1 |
|
V2 |
1 |
-1 |
0 |
-1 |
|
V3 |
0 |
1 |
-1 |
0 |
Т. е. 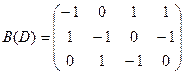
Если граф имеет кратные дуги (ребра), то в матрице смежности принимается Aij=K, где K – кратность дуги (ребра).
С помощью матриц смежности и инциндентности всегда можно полностью определеить граф и все его компоненты. Такой метод задания графов очень удобен для обработки данных на ЭВМ.
Пример. Задана симметрическая матрица Q неотрицательных чисел. Нарисовать на плоскости граф G(V, X), имеющий заданную матицу Q своей матрицей смежности. Найти матрицу инциндентности R графа G. Нарисованть также орграф ![]() , имеющий матрицу смежности Q, определить его матрицу инциндентности С.
, имеющий матрицу смежности Q, определить его матрицу инциндентности С.
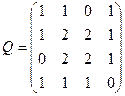
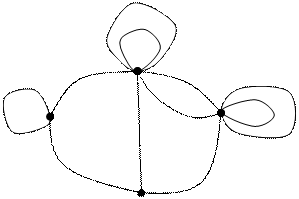 X4
X4
x3
v2
x2 x5
x6
x1 v1 v3 x7 x8
x10
x11 x9
v4
Составим матрицу инциндентности:
|
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
X9 |
X10 |
X11 |
|
|
V1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
V2 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
V3 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
|
V4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
Итого: 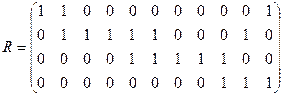
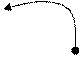
Построим теперь ориентированный граф с заданной матрицей смежности.
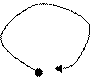
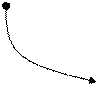




![]() X4
X4
x5

 v2
v2
![]()

 x2 x7
x2 x7

 х3 x6
х3 x6

 x1 v1 х8 v3 x10 x11
x1 v1 х8 v3 x10 x11
х9
х17 х15 x14
x16 х13 x12
v4
Составим матрицу инциндентности для ориетированного графа.
Элемент матрицы равен 1, если точка является концом дуги, -1 – если началом дуги, если дуга является петлей, элемент матрицы запишем как ±1.
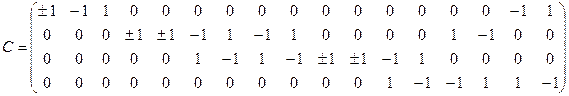
Таким образом, операции с графами можно свести к операциям с их матрицами.
| < Предыдущая | Следующая > |
|---|