01. Линейная алгебра. Основные определения. Действия над матрицами.

Определение. Матрицей размера m´n, где m - число строк, n - число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i - номер строки, а j - номер столбца.

А =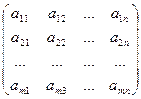

Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.

Определение. Если число столбцов матрицы равно числу строк (m=n), то матрица называется Квадратной.

Определение. Матрица вида:

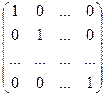= E,

Называется Единичной матрицей.

Определение. Если Amn = Anm , то матрица называется Симметрической.

Пример. - симметрическая матрица

Определение. Квадратная матрица вида 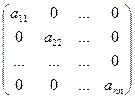называется Диагональной Матрицей.

Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они Определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц:

Определение. Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.

Cij = aij ± bij

С = А + В = В + А.

Операция Умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.

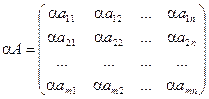
A (А+В) =aА ± aВ

А(a±b) = aА ± bА

Пример. Даны матрицы А = 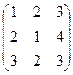; B = , найти 2А + В.

2А = 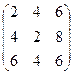, 2А + В = .

Следующая >