84. Элементы теории поля

Определение. Если каждой точке пространства М ставится в соответствие некоторая скалярная величина U, то таким образом задается Скалярное поле U(M). Если каждой пространства М ставится в соотвтствие вектор , то задается Векторное поле (М).

Пусть в пространстве М задана поверхность D. Будем считать, что в каждой точке Р определяется положительное направление нормали единичным вектором .

В пространстве М зададим векторное поле, постовив в соответствие каждой точке точке пространства вектор, определенный координатами:

Если разбить каким – либо образом поверхность на частичные участки Di и составить сумму , где - скалярное произведение, то предел этой суммы при стремлении к нулю площадей частичных участков разбиения (если этот предел существует) будет Поверхностным интегралом.

Определение. Поверхностный интеграл называется Потоком векторного поля через поверхность D.

Если поверхность разбита на конечное число частичных поверхностей, то поток векторного поля через всю поверхность будет равен сумме потоков через частичные поверхности.

Если преобразовать скалярное произведение в координатную форму, то получаем соотношение:

Если на области D существует функция F(X, Y, Z), имеющая непрерывные частные производные, для которых выполняются свойства:

То такую функцию называют Потенциальной функцией или ПОтенциалом Вектора .

Тогда вектор является Градиентом функции F.

Потенциал может быть найден по формуле:

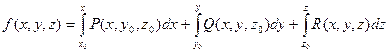
В этой формуле x0, y0, z0 – координаты некоторой начальной точки. В качестве такой точки удобно брать начало координат.

Теорема. Для того, чтобы поле вектора , заданного в некоторой области, имело потенциал, необходимо и достаточно, чтобы выполнялось одно из двух условий:

1) Интеграл от вектора по любому кусочно – гладкому контуру, принадлежащему области, равен нулю.

2) Интеграл по любому кусочно – гладкому пути, соединяющему две любые точки поля не зависит, от пути интегрирования.

< Предыдущая		Следующая >