77. Свойства криволинейного интеграла второго рода

1) Криволинейный интеграл при перемене направления кривой меняет знак.

2)

3)

4)

5) Криволинейный интеграл по замкнутой кривой L не зависит от выбора начальной точки, а зависит только от направления обхода кривой.

Направление обхода контура L задается дополнительно. Если L – замкнутая кривая без точек самопересечения, то направление обхода контура против часовой стрелки называется положительным.

6) Если АВ – кривая, лежащая в плоскости, перпендикулярной оси ОХ, то

Аналогичные соотношения справедливы при интегрировании по переменным У И Z.

Теорема. Если кривая АВ – кусочно - гладкая, а функции P(X, Y, Z), Q(X, Y, Z) и

R(X, Y, Z) – непрерывны на кривой АВ, то криволинейные интегралы

Существуют.

Вычисление криволинейных интегралов второго рода производится путем преобразования их к определенным интегралам по формулам:

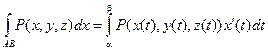
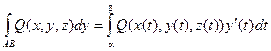
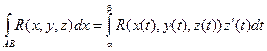
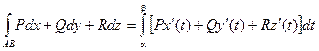
В случае, если АВ – плоская кривая, заданная уравнением Y = F(X), то

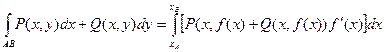
Пример. Вычислить криволинейный интеграл . L – контур, ограниченный параболами . Направление обхода контура положительное.

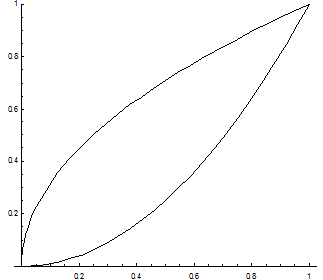
Представим замкнутый контур L как сумму двух дуг L1 = X2 и

< Предыдущая		Следующая >