73. Теоремы свертки и запаздывания
Теорема. (теорема запаздывания) Если F(T) = 0 при T < 0, то справедлива формула
Где T0 – некоторая точка.
Определение. Выражение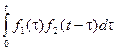 
называется Сверткой Функций F1(T) и F2(T) и обозначается F1* F2.
Теорема. (теорема свертки) Преобразование Лапласа от свертки равно произведению преобразований Лапласа от функций F1(T) и F2(T) .
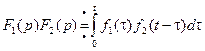
Теорема. (Интеграл Дюамеля (Дюамель (1797 – 1872) – французский математик)). Если 
, то верно равенство
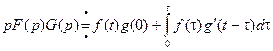
Для нахождения изображений различных функций наряду с непосредственным интегрированием применяются приведенные выще теоремы и свойства.
Пример. Найти изображение функции 
.
Из таблицы изображений получаем: 
.
По свойству интегрирования изображения получаем: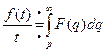 
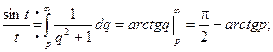
Пример. Найти изображение функции 
.
Из тригонометрии известна формула 
.
Тогда 
=
.
Операционное исчисление используется как для нахождения значений интегралов, так и для решение дифференциальных уравнений.
Пусть дано линейное дифференциальное уравнение с постоянными коэффициентами.
Требуется найти решение этого дифференциального уравнения, удовлетворяющее начальным условиям:
Если функция x(t) является решением этого дифференциального уравнения, то оно обращает исходное уравнение в тождество, значит функция, стоящая в левой части уравнения и функция f(t) имеет (по теореме единственности) одно и то же изображение Лапласа.
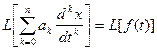
Из теоремы о дифференцировании оригинала {
} можно сделать вывод, что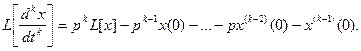 
Тогда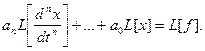 
Обозначим 
Получаем: 
Это уравнение называется Вспомогательным (изображающим) Или операторным уравнением.
Отсюда получаем изображение 
, а по нему и искомую функцию X(T).
Изображение получаем в виде: 
Где 
Этот многочлен зависит от начальных условий. Если эти условия нулевые, то многочлен равен нулю, и формула принимает вид:
Рассмотрим применение этого метода на примерах.
Изображение искомой функции будем искать в виде:
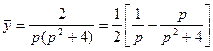
Находим оригинал, т. е. искомую функцию: 
Пример. Решить уравнение 
Пример. Решить уравнение:
Изображение искомой функции 
Для нахождения оригинала необходимо разложить полученную дробь на элементарные дроби. Воспользуемся делением многочленов (знаменатель делится без остатка на P – 1):
P3 – 6p2 + 11p – 6 p - 1
p3 – p2 p2 – 5p + 6
-5p2 + 11p
-5p2 + 5p
6p - 6
6p - 6
0
В свою очередь 
Получаем: 
Тогда: 
Определим коэффициенты А, В и С.
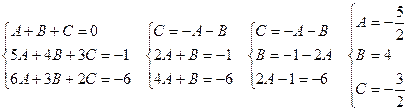
Тогда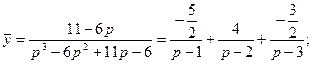 
Приемы операционного исчисления можно также использовать для решения систем дифференциальных уравнений.
Пример. Решить систему уравнений:
Обозначим 
- изображения искомых функций и решим вспомогательные уравнения:
Решим полученную систему алгебраических уравнений.
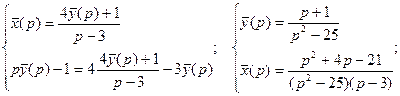
Если применить к полученным результатам формулы
То ответ можно представить в виде:
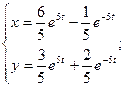
Как видно, гиперболические функции в ответе могут быть легко заменены на показательные.
Пример. Решить систему уравнений
при X(0) = Y(0) = 1
Составим систему вспомогательных уравнений:
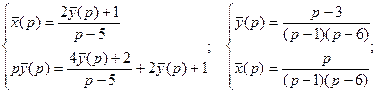
Если обозначить 
то из полученного частного решения системы можно записать и общее решение:
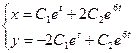
При рассмотрении нормальных систем дифференциальных уравнений этот пример был решен традиционным способом (См. Другой способ решения.). Как видно, результаты совпадают.
Отметим, что операторный способ решения систем дифференциальных уравнений применим к системам порядка выше первого, что очень важно, т. к. в этом случае применение других способов крайне затруднительно.
| < Предыдущая | Следующая > |
|---|
