70. Операционное исчисление. Преобразование Лапласа
(Пьер Симон Лаплас (1749 – 1825) – французский математик)
Рассмотрим функцию действительного переменного t, определенную при t ³ 0. Будем также считать, что функция f(t)- кусочно - непрерывная, т. е. в любом конечном интервале она имеет конечное число точек разрыва первого рода, и определена на бесконечном интервале (-¥, ¥), но f(t) = 0 при t < 0.
Будем считать, что функция ограничена условием:
![]()
Рассмотрим функцию
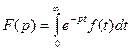
где p = a + ib – комплексное число.
Определение. Функция F(p) называется Изображением Лапласа Функции f(t).
Также функцию F(p) называют L – изображением Или Преобразованием Лапласа.
Обозначается ![]()
При этом функция f(t) называется Начальной функцией Или Оригиналом, а процесс нахождения оригинала по известному изображению называется Операционным исчислением.
Теорема. (Теорема единственности) Если две непрерывнные функции F(X) и G(X) имеют одно и то же L – изображение F(P), то они тождественно равны.
Определение. Функцией Хевисайда (Оливер Хевисайд (1850 – 1925) – английский физик) называется функция
![]()
| < Предыдущая | Следующая > |
|---|