59. Интеграл Фурье

Пусть функция F(X) на каждом отрезке [-L,L], где L – любое число, кусочно – гладкая или кусочно – монотонная, кроме того, F(X) – абсолютно интегрируемая функция, т. е. сходится несобственный интеграл

Тогда функция F(X) разлагается в ряд Фурье:

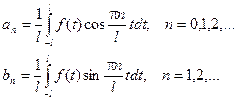
Если подставить коэффициенты в формулу для f(x), получим:

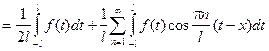
Переходя к пределу при L®¥, можно доказать, что 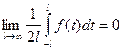и

Обозначим

При L®¥ DUn ®0.

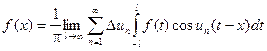
Можно доказать, что предел суммы, стоящий в правой части равенства равен интегралу

Тогда - Двойной интеграл Фурье.

Окончательно получаем:

- представление функции f(x) Интегралом Фурье.

Двойной интеграл Фурье для функции f(x) можно представить в комплексной форме:

< Предыдущая		Следующая >