55. Разложение в ряд Фурье непериодической функции

Задача разложения непериодической функции в ряд Фурье в принципе не отличается от разложения в ряд Фурье периодической функции.

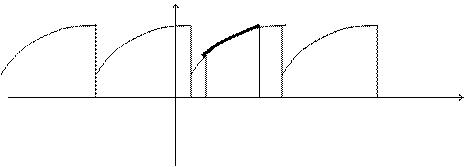
Допустим, функция F(X) задана на отрезке [a, b] и является на этом отрезке кусочно – монотонной. Рассмотрим произвольную периодическую кусочно – монотонную функцию F1(X) c периодом 2Т ³ ïB-Aï, совпадающую с функцией f(x) на отрезке [a, b].

y

f(x)

a - 2T a a b a+2T a + 4T x

Таким образом, функция F(X) была дополнена. Теперь функция F1(X) разлагается в ряд Фурье. Сумма этого ряда во всех точках отрезка [a, b] совпадает с функцией F(X), т. е. можно считать, что функция F(X) разложена в ряд Фурье на отрезке [a, b].

Таким образом, если функция f(x) задана на отрезке, равном 2p ничем не отличается от разложения в ряд периодической функции. Если же отрезок, на котором задана функция, меньше, чем 2p, то функция продолжается на интервал (b, a + 2p) так, что условия разложимости в ряд Фурье сохранялись.

Вообще говоря, в этом случае продолжение заданной функции на отрезок (интервал) длиной 2p может быть произведено бесконечным количеством способов, поэтому суммы получившихся рядов будут различны, но они будут совпадать с заданной функцией f(x) на отрезке [a, b].

< Предыдущая		Следующая >