39. Признак Коши. (радикальный признак)

Если для ряда С неотрицательными членами существует такое число Q<1, что для всех достаточно больших N Выполняется неравенство

,

То ряд Сходится, если же для всех достаточно больших N выполняется неравенство

То ряд Расходится.

Следствие. Если существует предел , то при r<1 ряд сходится, а при r>1 ряд расходится.

Пример. Определить сходимость ряда .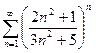

Вывод: ряд сходится.

Пример. Определить сходимость ряда .

Т. е. признак Коши не дает ответа на вопрос о сходимости ряда. Проверим выполнение необходимых условий сходимости. Как было сказано выше, если ряд сходится, то общий член ряда стремится к нулю.

,

Таким образом, необходимое условие сходимости не выполняется, значит, ряд расходится.

< Предыдущая		Следующая >