31. Решение задачи Дирихле для круга

Пусть в плоскости XOY имеется круг радиуса R с центром в начале координат и на его окружности задана функция F(J), Где J - полярный угол.

Требуется найти функцию , которая удовлетворяет уравнению Лапласа

И при

Запишем уравнение Лапласа в полярных координатах:

Полагаем Подставляя это соотношение в уравнение Лапласа, получаем:

Таким образом, имеем два уравнения:

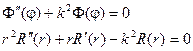
Общее решение первого уравнения имеет вид:

Решение второго уравнения ищем в виде: . При подстановке получим:

Общее решение второго уравнения имеет вид: .

Подставляя полученные решения в уравнение , получим:

Эта функция будет решением уравнения Лапласа при любом K ¹ 0.

Если K = 0, то следовательно .

Решение должно быть периодическим, т. к. одно и то же значение будет повторяться через 2p. (Тогда рассматривается одна и та же точка круга.) Поэтому В0 = 0.

Решение должно быть конечным и непрерывным, поэтому D0 = 0.

Окончательно получаем:

При этом:

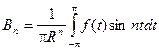
Если подставить эти коэффициенты в полученную выше формулу и произвести упрощение, получаем окончательный результат решения задачи Дирихле, который называется Интегралом Пуассона.

(Симеон Дени Пуассон (1781 – 1840) – французский математик)

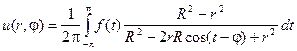
< Предыдущая		Следующая >