22. Линейные неоднородные дифференциальные уравнения с постоянными
Коэффициентами.
Уравнения с правой частью специального вида.
Представляется возможным представить вид частного решения в зависимости от вида правой части неоднородного уравнения.
Различают следующие случаи:
![]()
I. Правая часть линейного неоднородного дифференциального уравнения имеет вид:
![]()
Где ![]() - многочлен степени M.
- многочлен степени M.
Тогда частное решение ищется в виде:
![]()
Здесь Q(X)- многочлен той же степени, что и P(X), но с неопределенными коэффициентами, а R – число, показывающее сколько раз число a является корнем характеристического уравнения для соответствующего линейного однородного дифференциального уравнения.
Пример. Решить уравнение ![]() .
.
Решим соответствующее однородное уравнение: ![]()
![]()
![]()
Теперь найдем частное решение исходного неоднородного уравнения.
Сопоставим правую часть уравнения с видом правой части, рассмотренным выше.
![]()
Частное решение ищем в виде: ![]() , где
, где ![]()
Т. е. ![]()
Теперь определим неизвестные коэффициенты А И В.
Подставим частное решение в общем виде в исходное неоднородное дифференциальное уравнение.
![]()
![]()
Итого, частное решение: ![]()
Тогда общее решение линейного неоднородного дифференциального уравнения:
![]()
![]()
II. Правая часть линейного неоднородного дифференциального уравнения имеет вид:
![]()
Здесь Р1(х) И Р2(х) – многочлены степени M1 и M2 соответственно.
Тогда частное решение неоднородного уравнения будет иметь вид:
![]()
Где число R показывает сколько раз число ![]() является корнем характеристического уравнения для соответствующего однородного уравнения, а Q1(X) И Q2(X) – многочлены степени не выше M, где M- большая из степеней M1 и M2.
является корнем характеристического уравнения для соответствующего однородного уравнения, а Q1(X) И Q2(X) – многочлены степени не выше M, где M- большая из степеней M1 и M2.
Заметим, что если правая часть уравнения является комбинацией выражений рассмотренного выше вида, то решение находится как комбинация решений вспомогательных уравнений, каждое из которых имеет правую часть, соответствующую выражению, входящему в комбинацию.
Т. е. если уравнение имеет вид: ![]() , то частное решение этого уравнения будет
, то частное решение этого уравнения будет ![]() Где У1 И У2 – частные решения вспомогательных уравнений
Где У1 И У2 – частные решения вспомогательных уравнений
![]() и
и ![]()
Для иллюстрации решим Рассмотренный выше пример другим способом.
Пример. Решить уравнение ![]()
Правую часть дифференциального уравнения представим в виде суммы двух функций F1(X) + F2(X) = X + (-SinX).
Составим и решим характеристическое уравнение: ![]()
1. Для функции F1(X) решение ищем в виде ![]() .
.
Получаем: ![]() Т. е.
Т. е. ![]()

Итого: ![]()
2. Для функции F2(X) решение ищем в виде: ![]() .
.
Анализируя функцию F2(X), получаем: ![]()
Таким образом, ![]()
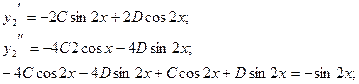
![]()
![]()
Итого: ![]()
Т. е. искомое частное решение имеет вид: ![]()
Общее решение неоднородного дифференциального уравнения:
![]()
Рассмотрим примеры применения описанных методов.
Пример. Решить уравнение ![]()
Составим характеристическое уравнение для соответствующего линейного однородного дифференциального уравнения:
![]()
Общее решение однородного уравнения: ![]()
Теперь найдем частное решение неоднородного уравнения в виде:
![]()
![]()
![]()
Воспользуемся методом неопределенных коэффициентов.
![]()
Подставляя в исходное уравнение, получаем:
![]()
![]()
Частное решение имеет вид: ![]()
Общее решение линейного неоднородного уравнения: ![]()
Пример. Решить уравнение ![]()
Характеристическое уравнение: ![]()
Общее решение однородного уравнения: ![]()
Частное решение неоднородного уравнения: ![]() .
.
![]()
![]()
Находим производные и подставляем их в исходное неоднородное уравнение:
![]()
![]()
![]()
![]()
Получаем общее решение неоднородного дифференциального уравнения:
![]()
Нормальные системы обыкновенных дифференциальных уравнений.
Определение. Совокупность соотношений вида:
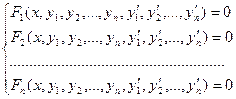
Где х - независимая переменная, У1, у2,…,уN – искомые функции, называется Системой дифференциальных уравнений первого порядка.
Определение. Система дифференциальных уравнений первого порядка, разрешенных относительно производных от неизвестных функций называется Нормальной системой дифференциальных уравнений.
Такая система имеет вид:
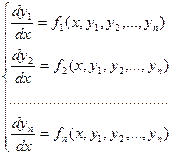 (1)
(1)
Для примера можно сказать, что график решения системы двух дифференциальных уравнений представляет собой интегральную кривую в трехмерном пространстве.
Теорема. (Теорема Коши). Если в некоторой области (N-1) –мерного пространства функции ![]()
![]() …
… ![]() непрерывны и имеют непрерывные частные производные по
непрерывны и имеют непрерывные частные производные по ![]() , то для любой точки
, то для любой точки ![]() этой области существует единственное решение
этой области существует единственное решение
![]()
Системы дифференциальных уравнений вида (1), определенное в некоторой окрестности точки х0 и удовлетворяющее начальным условиям ![]()
Определение. Общим решением Системы дифференциальных уравнений вида (1) будет совокупность функций ![]() ,
, ![]() , …
, … ![]() , которые при подстановке в систему (1) обращают ее в тождество.
, которые при подстановке в систему (1) обращают ее в тождество.
| < Предыдущая | Следующая > |
|---|