18. Линейные однородные дифференциальные уравнения с произвольными коэффициентами
Определение. Выражение 
называется Линейным дифференциальным оператором.
Линейный дифференциальный оператор обладает следующими свойствами:
1) 
2) 
Решения линейного однородного уравнения обладают следующими свойствами:
1) Если функция У1 является решением уравнения, то функция Су1, где С – постоянное число, также является его решением.
2) Если функции У1 И У2 являются решениями уравнения, то У1 +у2 также является его решением.
Структура общего решения.
Определение. Фундаментальной системой решений Линейного однородного дифференциального уравнения N –го порядка на интервале (a, b) называется всякая система N линейно независимых на этом интервале решений уравнения.
Определение. Если из функций Yi составить определитель N – го порядка
,
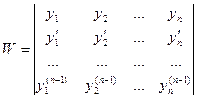То этот определитель называется Определителем Вронского.
( Юзеф Вроньский (1776 – 1853) – польский математик и философ - мистик)
Теорема. Если функции 
линейно зависимы, то составленный для них определитель Вронского равен нулю.
Теорема. Если функции Линейно независимы, то составленный для них определитель Вронского не равен нулю ни в одной точке рассматриваемого интервала.
Теорема. Для того, чтобы система решений линейного однородного дифференциального уравнения была фундаментальной необходимо и достаточно, чтобы составленный для них определитель Вронского был не равен нулю.
Теорема. Если - фундаментальная система решений на интервале (A, B), то общее решение линейного однородного дифференциального уравнения является линейной комбинацией этих решений.
,
Где Ci –Постоянные коэффициенты.
Применение приведенных выше свойств и теорем рассмотрим на примере линейных однородных дифференциальных уравнений второго порядка.
| < Предыдущая | Следующая > |
|---|
