14. Линейные неоднородные дифференциальные уравнения. Метод Бернулли

(Якоб Бернулли (1654-1705) – швейцарский математик.)

Для интегрирования линейных неоднородных уравнений (Q(X)¹0) применяются в основном два метода: метод Бернулли и метод Лагранжа.

Суть метода заключается в том, что искомая функция представляется в виде произведения двух функций .

При этом очевидно, что - дифференцирование по частям.

Подставляя в исходное уравнение, получаем:

Далее следует важное замечание – т. к. первоначальная функция была представлена нами в виде произведения, то каждый из сомножителей, входящих в это произведение, может быть произвольным, выбранным по нашему усмотрению.

Например, функция может быть представлена как

и т. п.

Таким образом, можно одну из составляющих произведение функций выбрать так, что выражение .

Таким образом, возможно получить функцию U, проинтегрировав, полученное соотношение как однородное дифференциальное уравнение по описанной выше схеме:

Для нахождения второй неизвестной функции V подставим поученное выражение для функции U В исходное уравнение с учетом того, что выражение, стоящее в скобках, равно нулю.

Интегрируя, можем найти функцию V:

; ;

Т. е. была получена вторая составляющая произведения , которое и определяет искомую функцию.

Подставляя полученные значения, получаем:

Окончательно получаем формулу:

, С2 - произвольный коэффициент.

Это соотношение может считаться решением неоднородного линейного дифференциального уравнения в общем виде по способу Бернулли.

Метод Лагранжа.

( Ларганж Жозеф Луи (1736-1813) - французский математик, през. Берлинской АН,

Поч. чл. Пет. АН (1776)).

Метод Лагранжа решения неоднородных линейных дифференциальных уравнений еще называют методом Вариации произвольной постоянной.

Вернемся к поставленной задаче:

Первый шаг данного метода состоит в отбрасывании правой части уравнения и замене ее нулем.

Далее находится решение получившегося однородного дифференциального уравнения:

.

Для того, чтобы найти соответствующее решение неоднородного дифференциального уравнения, будем считать постоянную С1 некоторой функцией от х.

Тогда по правилам дифференцирования произведения функций получаем:

Подставляем полученное соотношение в исходное уравнение

Из этого уравнения определим переменную функцию С1(х):

Интегрируя, получаем:

Подставляя это значение в исходное уравнение, получаем:

.

Таким образом, мы получили результат, полностью совпадающий с результатом расчета по методу Бернулли.

При выборе метода решения линейных дифференциальных уравнений следует руководствоваться простотой интегрирования функций, входящих в исходный интеграл.

Далее рассмотрим примеры решения различных дифференциальных уравнений различными методами и сравним результаты.

Пример. Решить уравнение

Сначала приведем данное уравнение к стандартному виду:

Применим полученную выше формулу:

Уравнение Бернулли.

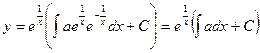
Определение. Уравнением Бернулли Называется уравнение вида

Где P и Q – функции от Х или постоянные числа, а N – постоянное число, не равное 1.

Для решения уравнения Бернулли применяют подстановку , с помощью которой, уравнение Бернулли приводится к линейному.

Для этого разделим исходное уравнение на Yn.

Применим подстановку, учтя, что .

Т. е. получилось линейное уравнение относительно неизвестной функции z.

Решение этого уравнения будем искать в виде:

Пример. Решить уравнение

Разделим уравнение на Xy2:

Полагаем

.

Полагаем

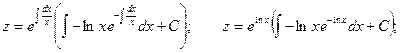
Произведя обратную подстановку, получаем:

Пример. Решить уравнение

Разделим обе части уравнения на

Полагаем

Получили линейное неоднородное дифференциальное уравнение. Рассмотрим соответствующее ему линейное однородное уравнение:

Полагаем C = C(x) и подставляем полученный результат в линейное неоднородное уравнение, с учетом того, что:

Получаем:

Применяя обратную подстановку, получаем окончательный ответ:

Уравнения в полных дифференциалах (тотальные).

Определение. Дифференциальное уравнение первого порядка вида:

Называется Уравнением в полных дифференциалах, если левая часть этого уравнения представляет собой полный дифференциал некоторой функции

Интегрирование такого уравнения сводится к нахождению функции U, после чего решение легко находится в виде:

Таким образом, для решения надо определить:

1) в каком случае левая часть уравнения представляет собой полный дифференциал функции U;

2) как найти эту функцию.

Если дифференциальная форма Является полным дифференциалом некоторой функции U, то можно записать:

Т. е. .

Найдем смешанные производные второго порядка, продифференцировав первое уравнение по У, а второе – по Х:

Приравнивая левые части уравнений, получаем Необходимое и достаточное условие того, что левая часть дифференциального уравнения является полным дифференциалом. Это условие также называется Условием тотальности.

Теперь рассмотрим вопрос о нахождении собственно функции U.

Проинтегрируем равенство :

Вследствие интегрирования получаем не постоянную величину С, а некоторую функцию С(у), т. к. при интегрировании переменная У полагается постоянным параметром.

Определим функцию С(у).

Продифференцируем полученное равенство по У.

Откуда получаем:

Для нахождения функции С(у) необходимо проинтегрировать приведенное выше равенство. Однако, перед интегрированием надо доказать, что функция С(у) не зависит от Х. Это условие будет выполнено, если производная этой функции по Х равна нулю.

Теперь определяем функцию С(у):

Подставляя этот результат в выражение для функции U, получаем:

Тогда общий интеграл исходного дифференциального уравнения будет иметь вид:

Следует отметить, что при решении уравнений в полных дифференциалах не обязательно использовать полученную формулу. Решение может получиться более компактным, если просто следовать методу, которым формула была получена.

Пример. Решить уравнение

Проверим условие тотальности:

Условие тотальности выполняется, следовательно, исходное дифференциальное уравнение является уравнением в полных дифференциалах.

Определим функцию U.

;

Итого,

Находим общий интеграл исходного дифференциального уравнения:

Уравнения вида Y = F(Y’) И X = F(Y’).

Решение уравнений, не содержащих в одном случае аргумента Х, а в другом – функции У, ищем в параметрической форме, принимая за параметр производную неизвестной функции.

Для уравнения первого типа получаем:

Делая замену, получаем:

В результате этих преобразований имеем дифференциальное уравнение с разделяющимися переменными.

Общий интеграл в параметрической форме представляется системой уравнений:

Исключив из этой системы параметр Р, получим общий интеграл и не в параметрической форме.

Для дифференциального уравнения вида X = F(Y’) с помощью той же самой подстановки и аналогичных рассуждений получаем результат:

Уравнения Лагранжа и Клеро.

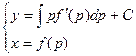
( Алекси Клод Клеро (1713 – 1765) французский математик

Ин. поч. член Петерб. АН )

Определение. Уравнением Лагранжа Называется дифференциальное уравнение, линейное относительно Х и У, коэффициенты которого являются функциями от Y’.

Для нахождения общего решение применяется подстановка P = Y’.

Дифференцируя это уравнение, c учетом того, что , получаем:

Если решение этого (линейного относительно Х) уравнения есть То общее решение уравнения Лагранжа может быть записано в виде:

Определение. Уравнением Клеро Называется уравнение первой степени (т. е. линейное) относительно функции и аргумента вида:

Вообще говоря, уравнение Клеро является частным случаем уравнения Лагранжа.

С учетом замены , уравнение принимает вид:

Это уравнение имеет два возможных решения:

или

В первом случае:

Видно, что общий интеграл уравнения Клеро представляет собой семейство прямых линий.

Во втором случае решение в параметрической форме выражается системой уравнений:

Исключая параметр Р, получаем второе решение F(x, y) = 0. Это решение не содержит произвольной постоянной и не получено из общего решения, следовательно, не является частным решением.

Это решение будет являться особым интегралом. ( См. Особое решение.)

Далее рассмотрим примеры решения различных типов дифференциальных уравнений первого порядка.

Пример. Решить уравнение с заданными начальными условиями.

Это линейное неоднородное дифференциальное уравнение первого порядка.

Решим соответствующее ему однородное уравнение.

Для неоднородного уравнения общее решение имеет вид:

Дифференцируя, получаем:

Для нахождения функции С(х) подставляем полученное значение в исходное дифференциальное уравнение:

Итого, общее решение:

C учетом начального условия Определяем постоянный коэффициент C.

Окончательно получаем:

Для проверки подставим полученный результат в исходное дифференциальное уравнение: верно

Ниже показан график интегральной кривой уравнения.

Пример. Найти общий интеграл уравнения .

Это уравнение с разделяющимися переменными.

Общий интеграл имеет вид:

Построим интегральные кривые дифференциального уравнения при различных значениях С.

С = - 0,5 С = -0,02 С = -1 С = -2

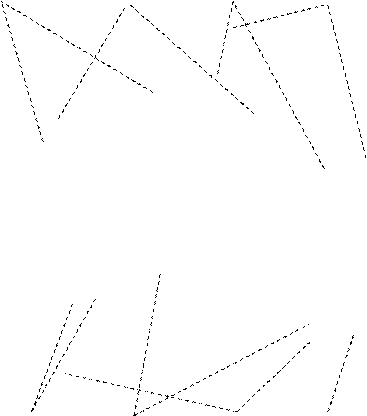
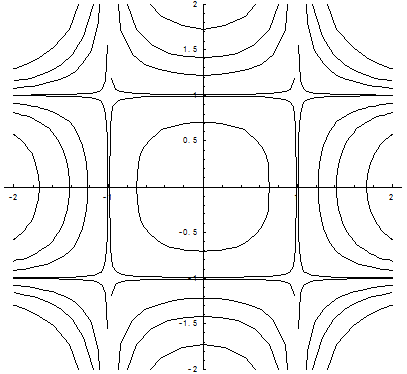
С = 0,02 С = 0,5 С = 1 С = 2

Пример. Найти решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.

Это уравнение с разделяющимися переменными.

Общее решение имеет вид:

Найдем частное решение при заданном начальном условии У(0) = 0.

Окончательно получаем:

Пример. Решить предыдущий пример другим способом.

Действительно, уравнение может быть рассмотрено как линейное неоднородное дифференциальное уравнение.

Решим соответствующее ему линейное однородное уравнение.

Решение неоднородного уравнения будет иметь вид:

Тогда

Подставляя в исходное уравнение, получаем:

Итого

С учетом начального условия у(0) = 0 получаем

Как видно результаты, полученные при решении данного дифференциального уравнения различными способами, совпадают.

При решении дифференциальных уравнений бывает возможно выбирать метод решения, исходя из сложности преобразований.

Пример. Решить уравнение С начальным условием у(0) = 0.

Это линейное неоднородное уравнение. Решим соответствующее ему однородное уравнение.

Для линейного неоднородного уравнения общее решение будет иметь вид:

Для определения функции С(х) найдем производную функции У и подставим ее в исходное дифференциальное уравнение.

Итого

Проверим полученное общее решение подстановкой в исходное дифференциальное уравнение.

(верно)

Найдем частное решение при у(0) = 0.

Окончательно

Пример. Найти решение дифференциального уравнения

С начальным условием у(1) = 1.

Это уравнение может быть преобразовано и представлено как уравнение с разделенными переменными.

С учетом начального условия:

Окончательно

Пример. Решить дифференциальное уравнение с начальным условием у(1) = 0.

Это линейное неоднородное уравнение.

Решим соответствующее ему однородное уравнение.

Решение неоднородного уравнения будет иметь вид:

Подставим в исходное уравнение:

Общее решение будет иметь вид:

C учетом начального условия у(1) = 0:

Частное решение:

Пример. Найти решение дифференциального уравнения с начальным условием у(1) = е.

Это уравнение может быть приведено к виду уравнения с разделяющимися переменными с помощью замены переменных.

Обозначим:

Уравнение принимает вид:

Получили уравнение с разделяющимися переменными.

Сделаем обратную замену:

Общее решение:

C учетом начального условия у(1) = е:

Частное решение:

Второй способ решения.

Получили линейное неоднородное дифференциальное уравнение. Соответствующее однородное:

Решение исходного уравнения ищем в виде:

Тогда

Подставим полученные результаты в исходное уравнение:

Получаем общее решение:

Пример. Решить дифференциальное уравнение с начальным условием у(1)=0.

В этом уравнении также удобно применить замену переменных.

Уравнение принимает вид:

Делаем обратную подстановку:

Общее решение:

C учетом начального условия у(1) = 0:

Частное решение:

Второй способ решения.

Замена переменной:

Общее решение:

< Предыдущая		Следующая >