09. Уравнения с разделяющимися переменными
Определение. Дифференциальное уравнение 
Называется Уравнением с разделяющимися переменными, если его можно записать в виде
.
Такое уравнение можно представить также в виде:
Перейдем к новым обозначениям 
Получаем: 
После нахождения соответствующих интегралов получается общее решение дифференциального уравнения с разделяющимися переменными.
Если заданы начальные условия, то при их подстановке в общее решение находится постоянная величина С, а, соответственно, и частное решение.
Пример. Найти общее решение дифференциального уравнения: 
Интеграл, стоящий в левой части, берется по частям (см. Интегрирование по частям.):
- это есть общий интеграл исходного дифференциального уравнения, т. к. искомая функция и не выражена через независимую переменную. В этом и заключается Отличие общего (частного) Интеграла от общего (частного) Решения.
Чтобы проверить правильность полученного ответа продифференцируем его по переменной х.
- верно
Пример. Найти решение дифференциального уравнения 
при условии у(2) = 1.
При у(2) = 1 получаем 
Итого: 
или 
- частное решение;
Проверка: 
, итого
- верно.
Пример. Решить уравнение 
- общий интеграл
- общее решение
Пример. Решить уравнение 
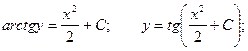
Пример. Решить уравнение 
При условии у(1) = 0.
Интеграл, стоящий в левой части будем брать по частям (см. Интегрирование по частям.).
Если у(1) = 0, то 
Итого, частный интеграл: 
.
Пример. Решить уравнение 
.
Для нахождения интеграла, стоящего в левой части уравнения см.Таблица основных интегралов. п.16. Получаем общий интеграл:
Пример. Решить уравнение 
Преобразуем заданное уравнение:
Получили общий интеграл данного дифференциального уравнения. Если из этого соотношения выразить искомую функцию у, то получим общее решение.
Пример. Решить уравнение 
.
; 
;
Допустим, заданы некоторые начальные условия х0 и у0. Тогда:
Получаем частное решение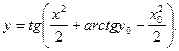 
| < Предыдущая | Следующая > |
|---|
