79. Замена переменных в двойном интеграле

Расмотрим двойной интеграл вида , где переменная х изменяется в пределах от a до b, а переменная у – от j1(x) до j2(х).

Положим х = f(u, v); y = j(u, v)

Тогда dx = ; dy = ;

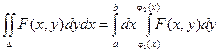
Т. к. при первом интегрировании переменная х принимается за постоянную, то dx = 0.

, т. е.

Пожставляя это выражение в записанное выше соотношение для dy, получаем:

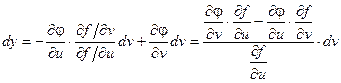
Выражение 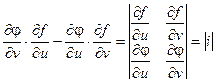называется Определителем Якоби Или Якобианом Функций f(u, v) и j(u, v).

(Якоби Карл Густав Якоб – (1804-1851) – немецкий математик)

Тогда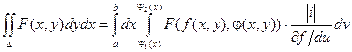

Т. к. при первом интегрировании приведенное выше выражение для dx принимает вид ( при первом интегрировании полагаем v = const, dv = 0), то при изменении порядка интегрирования, получаем соотношение:

< Предыдущая		Следующая >