78. Вычисление двойного интеграла

Теорема. Если функция F(X, Y) непрерывна в замкнутой области D, ограниченной линиями х = A, X = B, (A < B), Y = J(X), Y = Y(X), где J и Y - непрерывные функции и

J £ Y, тогда

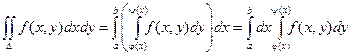
y y = y(x)

D

y = j(x)

a b x

Пример. Вычислить интеграл , если область D ограничена линиями: y = 0, y = x2, x = 2.

y

4

D

0 2 x

=

=

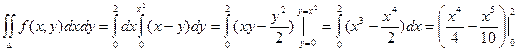Теорема. Если функция F(X, Y) непрерывна в замкнутой области D, ограниченной линиями Y = C, Y = D (C < D), X = F(Y), X = Y(Y) (F(Y) £ Y(Y)), то

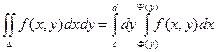
Пример. Вычислить интеграл , если область D ограничена линиями y = x, x = 0, y = 1, y = 2.

y

y = x

2

D

1

0 x

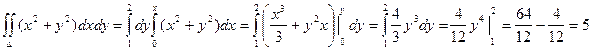
Пример. Вычислить интеграл , если область интегрирования D ограничена линиями х = 0, х = у2, у = 2.

=

=

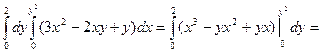
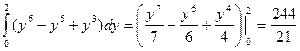
Пример. Вычислить двойной интеграл , если область интегрирования ограничена линиями ху=1, у = , х = 2.

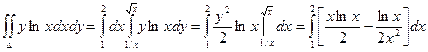
1.

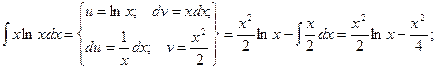
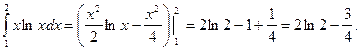
2.

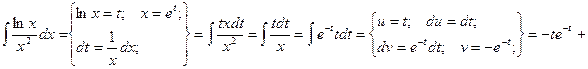
3.

При использовании компьютерной версии “Курса высшей математики” возможно запустить программу, которая вычисляет двойной интеграл от любой функции.

Для запуска программы дважды щелкните на значке

Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (Ó Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.

< Предыдущая		Следующая >