53. Формула прямоугольников
Если известны значения функции f(x) в некоторых точках x0, x1, … , xm, то в качестве функции “близкой” к f(x) можно взять многочлен Р(х) степени не выше m, значения которого в выбранных точках равны значениям функции f(x) в этих точках.
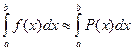
Если разбить отрезок интегрирования на n равных частей ![]() . При этом:
. При этом:
Y0 = f(x0), y1 = f(x1), …. , yn = f(xn).
Составим суммы: y0Dx + y1Dx + … + yn-1Dx
y1Dx + y2Dx + … + ynDx
Это соответственно нижняя и верхняя интегральные суммы. Первая соответствует вписанной ломаной, вторая – описанной.
Тогда 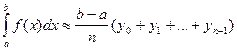 или
или
 - любая из этих формул может применяться для приближенного вычисления определенного интеграла и называется Общей формулой прямоугольников.
- любая из этих формул может применяться для приближенного вычисления определенного интеграла и называется Общей формулой прямоугольников.
| < Предыдущая | Следующая > |
|---|