36. Кривизна пространственной кривой

z

A(x, y, z)

B

0 y

x

Для произвольной точки А, находящейся на пространственной кривой, координаты могут быть определены как функции некоторой длины дуги S.

X = j(S); y = y(S); z = f(S);

Приведенное выше уравнение называют Векторным уравнением линии в пространстве.

Определение: Линия, которую опишет в пространстве переменный радиус – вектор При изменении параметра S, называется Годографом этого вектора.

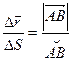, тогда - вектор, направленный по касательной к кривой в точке А(x, y, z).

Но т. к. 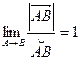, то - единичный вектор, направленный по касательной.

Если принять , то .

Причем .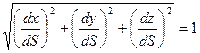

Рассмотрим вторую производную

Определение: Прямая, имеющая направление вектора Называется Главной нормалью к кривой. Ее единичный вектор обозначается .

, где К – кривизна кривой.

Кривизна пространственной кривой может быть найдена по формуле:

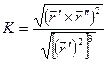
Возможна и другая запись формулы для кривизны пространственной кривой (она получается из приведенной выше формулы):

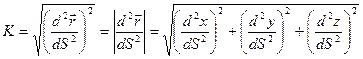
Определение: Вектор называется Вектором кривизны. Величина называется Радиусом кривизны.

< Предыдущая		Следующая >