35. Свойства эволюты

Теорема 1: Нормаль к данной кривой является касательной к ее эволюте.

Теорема 2: Модуль разности радиусов кривизны в любых точках кривой равен модулю длины соответствующей эволюты.

С3

С2

С1

R1 R2 R3

M1

M’1 M2 M3

M’2

M’3

Надо отметить, что какой – либо эволюте соответствует бесконечное число эвольвент.

Указанные выше свойства можно проиллюстрировать следующим образом: если на эволюту натянута нить, то эвольвента получается как траекторная линия конца нити при ее сматывании или разматывании при условии, что нить находится в натянутом состоянии.

Пример: Найти уравнение эволюты кривой, заданной уравнениями:

Уравнения эволюты: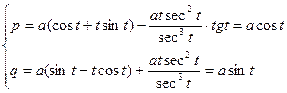

Окончательно: - это уравнения окружности с центром в начале координат радиуса а. Исходная кривая получается своего рода разверткой окружности.

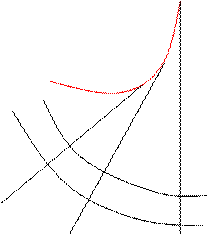
Ниже приведены графики исходной кривой и ее эволюты.

< Предыдущая		Следующая >