33. Производная функции, заданной параметрически
Пусть ![]()
Предположим, что эти функции имеют производные и функция x = j(t) имеет обратную функцию t = Ф(х).
Тогда функция у = y(t) может быть рассмотрена как сложная функция y = y[Ф(х)].
![]()
Т. к. Ф(х) – обратная функция, то 
Окончательно получаем: 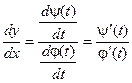
Таким образом, можно находить производную функции, не находя непосредственной зависимости у от х.
Пример. Найти производную функции ![]()
Способ 1: Выразим одну переменную через другую ![]() , тогда
, тогда
![]()
Способ 2: Применим параметрическое задание данной кривой: ![]() .
.
![]()
X2 = a2cos2t; ![]()
![]()
![]()
| < Предыдущая | Следующая > |
|---|