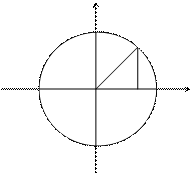
32. Уравнения некоторых типов кривых в параметрической форме

Окружность.

Если центр окружности находится в начале координат, то координаты любой ее

Точки могут быть найдены по формулам:

0 £ t £ 3600

Если исключить параметр t, то получим каноническое уравнение окружности:

X2 + y2 = r2(cos2t + sin2t) = r2

Эллипс.

Каноническое уравнение: .

В

C M(x, y)

T

О N P

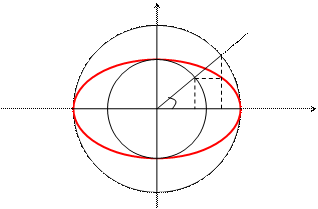
Для произвольной точки эллипса М(х, у) из геометрических соображений можно записать: из DОВР и из DOCN, где а - большая полуось эллипса, а b - меньшая полуось эллипса, х и у – координаты точки М.

Тогда получаем параметрические уравнения эллипса:

где 0 £ t £ 2p

Угол t называется Эксцентрическим углом.

Циклоида.

у

С

М К

О Р В pа 2pа х

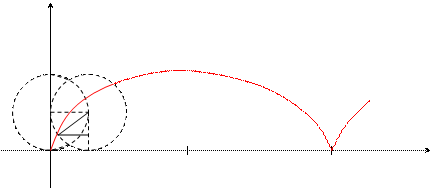
Определение. Циклоидой называется кривая, которую описывает некоторая точка, лежащая на окружности, когда окружность без скольжения катится по прямой.

Пусть окружность радиуса а перемещается без скольжения вдоль оси х. Тогда из геометрических соображений можно записать: OB = = at; PB = MK = asint;

ÐMCB = t; Тогда y = MP = KB = CB – CK = a – acost = a(1 – cost).

X = at – asint = a(t – sint).

Итого: при 0 £ t £ 2p - это параметрическое уравнение циклоиды.

Если исключить параметр, то получаем:

Как видно, параметрическое уравнение циклоиды намного удобнее в использовании, чем уравнение, непосредственно выражающее одну координату через другую.

Астроида.

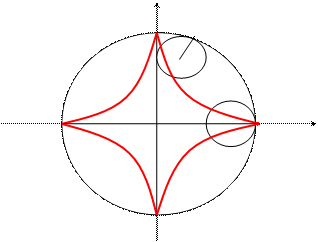
Данная кривая представляет собой траекторию точки окружности радиуса R/4, вращающейся без скольжения по внутренней стороне окружности радиуса R.

R/4

R

Параметрические уравнения, задающие изображенную выше кривую,

, 0 £ t £ 2p,

Преобразуя, получим: x2/3 + y2/3 = a2/3(cos2t + sin2t) = a2/3

< Предыдущая		Следующая >