18. Теорема Лагранжа
(Жозеф Луи Лагранж (1736-1813) французский математик)
Если функция F(X) непрерывна на отрезке [A, B] и дифференцируема на интервале (а, B), то на этом интервале найдется по крайней мере одна точка E
Это означает, что если на некотором промежутке выполняются условия теоремы, то отношение приращения функции к приращению аргумента на этом отрезке равно значению производной в некоторой промежуточной точке.
Рассмотренная выше теорема Ролля является частным случаем теоремы Лагранжа.
Отношение![]() равно угловому коэффициенту секущей АВ.
равно угловому коэффициенту секущей АВ.
 у
у
В
А
0 а e b x
Если функция f(x) удовлетворяет условиям теоремы, то на интервале (а, b) существует точка e такая, что в соответствующей точке кривой y = f(x) касательная параллельна секущей, соединяющей точки А и В. Таких точек может быть и несколько, но одна существует точно.
Доказательство. Рассмотрим некоторую вспомогательную функцию
F(X) = F(X) – Yсек АВ
Уравнение секущей АВ можно записать в виде:
![]()
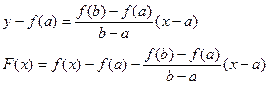
Функция F(x) удовлетворяет теореме Ролля. Действительно, она непрерывна на отрезке [a, b] и дифференцируема на интервале (а, b). По теореме Ролля существует хотя бы одна точка e, a < e < b, такая что F¢(e) = 0.
Т. к. ![]() , то
, то ![]() , следовательно
, следовательно
![]()
Теорема доказана.
Определение. Выражение ![]() называется Формулой
называется Формулой
Лагранжа Или Формулой конечных приращений.
В дальнейшем эта формула будет очень часто применяться для доказательства самых разных теорем.
Иногда формулу Лагранжа записывают в несколько другом виде:
![]() ,
,
Где 0 < q < 1, Dx = b – a, Dy = f(b) – f(a).
| < Предыдущая | Следующая > |
|---|