13. Формула Тейлора

Тейлор (1685-1731) – английский математик

Теорема Тейлора. 1) Пусть функция F(X) имеет в точке х = а и некоторой ее окрестности производные порядка до (N+1) включительно.{ Т. е. и все предыдущие до порядка N Функции и их производные непрерывны и дифференцируемы в этой окрестности}.

2) Пусть х - любое значение из этой окрестности, но х ¹ а.

Тогда между точками х и а найдется такая точка E, что справедлива формула:

- это выражение называется Формулой Тейлора, а выражение:

Называется Остаточным членом в форме Лагранжа.

Доказательство. Представим функцию f(x) в виде некоторого многочлена Pn(x), значение которого в точке х = а равно значению функции f(x), а значения его производных равно значениям соответствующих производных функции в точке х = а.

(1)

Многочлен Pn(x) будет близок к функции f(x). Чем больше значение n, тем ближе значения многочлена к значениям функции, тем точнее он повторяет функцию.

Представим этот многочлен с неопределенными пока коэффициентами:

(2)

Для нахождения неопределенных коэффициентов вычисляем производные многочлена в точке х = а и составляем систему уравнений:

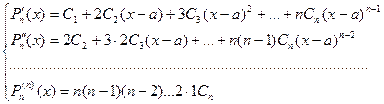(3)

Решение этой системы при х = а не вызывает затруднений, получаем:

…………………….

Подставляя полученные значения Ci в формулу (2), получаем:

Как было замечено выше, многочлен не точно совпадает с функцией f(x), т. е. отличается от нее на некоторую величину. Обозначим эту величину Rn+1(x). Тогда:

F(x) = Pn(x) + Rn+1(x)

Теорема доказана.

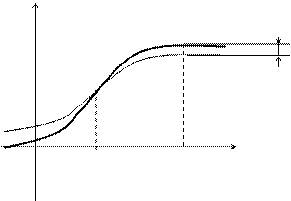
Рассмотрим подробнее величину Rn+1(x).

y Как видно на рисунке, в

точке х = а значение многочлена f(x)=Rn+1(x) в точности совпадает со значением функции.

Pn(x) Однако, при удалении от точки х = а расхождение значений увеличивается.

 

Иногда используется другая запись для Rn+1(x). Т. к. точка eÎ(a, x), то найдется такое число q из интервала 0 < q < 1, что e = a + q(x – a).

Тогда можно записать:

Тогда, если принять a = x0, x – a = Dx, x = x0 + Dx, формулу Тейлора можно записать в виде:

Где 0 < q < 1

Если принять n =0, получим: F(X0 + DX) – F(X0) = F¢(X0 + QDX)×DX – это выражение называется Формулой Лагранжа. (Жозеф Луи Лагранж (1736-1813) французский математик и механик).

Формула Тейлора имеет огромное значение для различных математических преобразований. С ее помощью можно находить значения различных функций, интегрировать, решать дифференциальные уравнения и т. д.

При рассмотрении Степенных рядов будет более подробно описаны некоторые особенности и условия разложения функции по формуле Тейлора.

< Предыдущая		Следующая >