48. Определение фориы связи и понятие регрессии

Определить форму связи между СВ – значит выявить механизм получения зависимой случайной величины. При изучении статистических связей, форму связей характеризует функция регрессии:

- зависимость условного МО

Если св Х и Y зависимы, то МО их произведения:

Регрессия св Y относительно Х определяется как:

,

где - условная плотность вероятности по формуле Байеса:

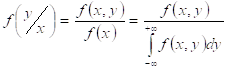
- регрессия Х по Y.

Функция регрессии имеет важное практическое значение. Она может быть использована для прогноза значений, которые может принимать известная случайная величина при ставших известными значениях другой случайной величины.

Точность прогноза определяется дисперсией условного распределения:

Учитывая:

Несмотря на важность функции регрессии, возможности ее практического использования ограничены, т. к. для ее вычисления необходимо знать аналитический вид двумерной функции {x, y}. Мы же, как правило, имеем выборку ограниченного объема.

Традиционный путь приводи к большим ошибкам, т. к. одну и ту же совокупность точек на плоскости можно описать с помощью различных функций.

Другой характеристикой формы связи, используемой на практике, стала Кривая регрессии – зависимость условного среднего случайной величины от значения, которое принимает случайная величина Х: .

Определение кривой регрессии инвариантно закона совместного распределения св Х и Y. Важное значение в практике Имеет двумерный нормальный закон распределения. Особенностью этого распределения является то, что условные МО совпадают с условными средними. При этом функция регрессии совпадает с кривой регрессии.

< Предыдущая		Следующая >