43. Критерий Колмогорова

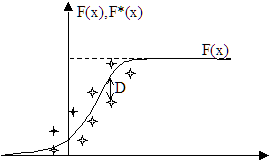
По результатам выборки объёмом n строится эмпирическая функция распределения F(х). Принимается гипотеза Н0: случайная величина Х подчиняется распределению описанному функцией F(x).

За меру расхождения функций принимается величина:

Существуют таблицы распределения Колмогорова в которых можно найти:

- критическое значение. Оно зависит от уровня значимости α(Р = 1 - α), величины D и величины выборки n.

Если полученные из опыта значения коэффициента D оказывается больше критического , то Н0 отвергается.

Если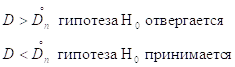

С помощью величины можно построить доверительные границы для неизвестной функции F(x):

Колмогоров показал, что при n → ∞ величина:

Подчиняется распределению Колмогорова.

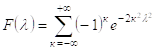
Критерий Колмогорова так же может быть использован для статистической проверки принадлежности двух выборок объёмом n1 и n2 к одной и той же генеральной совокупности. Вычисляется параметр λ:

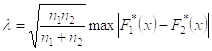
Где: - эмпирические функции распределения соответственно первой и второй выборки.

По величине λ судят о согласии.

< Предыдущая		Следующая >