42. Критерий согласия χ2 Пирсона

Имеется случайная величина Х, выдвигается гипотеза Н0: F(x), делается выборка.

Диапазон Хmin – Хmax разбивается на ℓ интервалов. Размер интервала определяется по правилу Старджесса. D1;D2;D3;…;Dℓ.

Интервал Di	D1	D2	D3	…	Dℓ
Эмпирическая частота mi	M1	M2	M3	…	Mℓ
Теоретическая частота npi	Np1	Np2	Np2	…	Npℓ

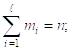
Mi > 3(в среднем 5 - 7).

При mi < 3 укрупнить интервал.

Находим частоту попадания случайной величины внутрь каждого интер­ва­ла.

Поскольку теоретическое распределение задано в гипотезе Н0 всегда можно найти вероятность pi попадания случайной величины внутрь каждого интервала.

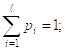
χ2 Пирсона предполагает, что надо построить:

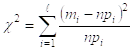
(имеет распределение χ2 только при относительно больших n (n > 50)).

Порядок применения χ2 Пирсона:

1. Рассчитывается эмпирическое значение критерия χ2;

2. Выбирается уровень значимости α (при Р = 1 - α);

3. По таблице подсчитывается ,

Где: α – уровень значимости;

к – число степеней свободы.

В общем случае к = ℓ - r – 1,

Где: ℓ - количество интервалов разбиения;

r – количество параметров распределения подсчитанных по выборке;

Здесь к = r – 1.

Если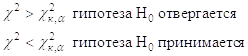

< Предыдущая		Следующая >