14. Бинарные операции (с несколькими величинами)

СВ X, Y заданы в 1 опыте.

Исход опыта	E1	E2	…	En
Вероятность исхода	P1	P2	…	Pn
X	X1	X2	…	Xn
Y	Y1	Y2	…	Yn
Z=J(XY)	Z1	Z2	…	Zn

Сложнее, если СВ задана только своим распределением:

X	A1	A2	…	An
Р	P1	P2	…	Pn

Y	B1	B2	…	Bn
Р	G1	G2	…	Gn

Z=X+Y

СВ Z принимает значения ak+bs, где ak=a1,a2,…,an; bs=b1,b2,…bm.

Общее количество возможных значений СВ = m×n.

P(Z=ak+bs)=P(X=ak, Y=bs)

Для нахождения такой вероятности необходимо знать закон совместного распределения СВ X и Y.

Набор точек (ak, bs) вместе с вероятностями P(X=ak, Y=bs) называется Совместным распределением СВ X и Y. Обычно такое распределение задается таблицей.

Определение закона распределения суммы СВ по законам распределения слагаемых называется Композицией законов распределения.

X \Y	B1	B12	…	Bs	…	Bm	Px
A1	P11	P12	…	P1s	…	P1m	P1
A2	P21	P22	…	P2s	…	P2m	P2
…	…	…	…	…	…	…	…
Ak	Pk1	…	…	Pks	…	Pkm	Pk
…	…	…	…	…	…	…	…
An	Pn1	Pn2	…	Pns	…	Pnm	Pn
Py	G1	G2	…	Gs	…	Gm	1

Наиболее просто вероятности Pks находятся в случае независимости СВ X и Y. Две СВ X и Y называются Независимыми тогда и только тогда, когда

P(X=ak, Y=bs)=P(X=ak)×P(Y=bs)

Pks=Pk×Ps

По известному закону распределения совместного распределения СВ X и Y могут быть найдены одномерные законы распределения СВ X и Y.

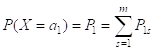
Теорема . Если СВ Х, Y являются независимыми, то любые функции j(Х) и y(У) от этих величин также являются независимыми.

< Предыдущая		Следующая >