12. Основные дискретные и непрерывные случайные величины

Дискретные случайные величины (ДСВ).

1. Биноминальная случайная величина x{0,1,2,3…n}

, p+q=1, 0<p<1

2. Пуассоновская случайная величина x{0,1,2,3…}

3. Бернуллиевая случайная величина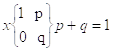

4. Равномерное распределение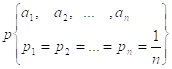

Непрерывные случайные величины (НСВ).

1. Равномерное распределение

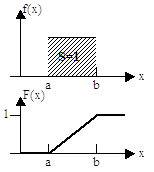
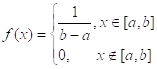
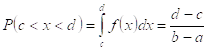
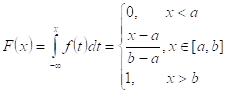
2. Треугольное распределение Симпсона

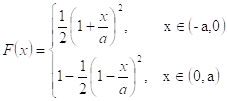
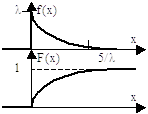3. Экспоненциальное (показательное) распределение. Имеет важное значение в теории массового обслуживания и теории надежности.

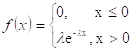
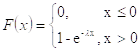
L - интенсивность.

3. Нормальный закон распределения.

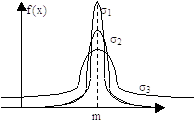
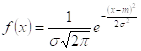, s>0

S=1, m=0 – нормальное стандартное распределение (m-мат. ожидание)

- такой подстановкой любое нормальное распределение приводится к стандартному.

При фиксированном s и изменяющемся m, кривая двигается вдоль Ох, не изменяя формы.

При фиксированном m и изменяющемся s (s1<s2<s3), кривая вытягивается вдоль оси ординат, но площадь фигуры под каждой кривой = 1.

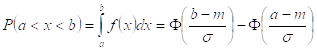
Функция Лапласа:

< Предыдущая		Следующая >